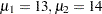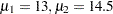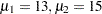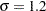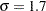| The POWER Procedure |
| Determining Required Sample Size for a Two-Sample t Test |
In this example you want to compare two physical therapy treatments designed to increase muscle flexibility. You need to determine the number of patients required to achieve a power of at least 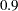 to detect a group mean difference in a two-sample
to detect a group mean difference in a two-sample  test. You will use
test. You will use 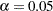 (two-tailed).
(two-tailed).
The mean flexibility with the standard treatment (as measured on a scale of 1 to 20) is well known to be about 13 and is thought to be between 14 and 15 with the new treatment. You conjecture three alternative scenarios for the means:
You conjecture two scenarios for the common group standard deviation:
You also want to try three weighting schemes:
equal group sizes (balanced, or 1:1)
twice as many patients with the new treatment (1:2)
three times as many patients with the new treatment (1:3)
This makes  scenarios in all.
scenarios in all.
Use the TWOSAMPLEMEANS statement in the POWER procedure to determine the sample sizes required to give 90% power for each of these 18 scenarios. Indicate total sample size as the result parameter by specifying the NTOTAL= option with a missing value (.). Specify your conjectures for the means by using the GROUPMEANS= option. Using the "matched" notation (discussed in the section Specifying Value Lists in Analysis Statements), enclose the two group means for each scenario in parentheses. Use the STDDEV= option to specify scenarios for the common standard deviation. Specify the weighting schemes by using the GROUPWEIGHTS= option. You could again use the matched notation. But for illustrative purposes, specify the scenarios for each group weight separately by using the "crossed" notation, with scenarios for each group weight separated by a vertical bar (|). The statements that perform the analysis are as follows:
proc power;
twosamplemeans
groupmeans = (13 14) (13 14.5) (13 15)
stddev = 1.2 1.7
groupweights = 1 | 1 2 3
power = 0.9
ntotal = .;
run;
Default values for the TEST=, DIST=, NULLDIFF=, ALPHA=, and SIDES= options specify a two-sided  test of group mean difference equal to 0, assuming a normal distribution with a significance level of
test of group mean difference equal to 0, assuming a normal distribution with a significance level of  = 0.05. The results are shown in Figure 68.4.
= 0.05. The results are shown in Figure 68.4.
| Fixed Scenario Elements | |
|---|---|
| Distribution | Normal |
| Method | Exact |
| Group 1 Weight | 1 |
| Nominal Power | 0.9 |
| Number of Sides | 2 |
| Null Difference | 0 |
| Alpha | 0.05 |
| Computed N Total | ||||||
|---|---|---|---|---|---|---|
| Index | Mean1 | Mean2 | Std Dev | Weight2 | Actual Power | N Total |
| 1 | 13 | 14.0 | 1.2 | 1 | 0.907 | 64 |
| 2 | 13 | 14.0 | 1.2 | 2 | 0.908 | 72 |
| 3 | 13 | 14.0 | 1.2 | 3 | 0.905 | 84 |
| 4 | 13 | 14.0 | 1.7 | 1 | 0.901 | 124 |
| 5 | 13 | 14.0 | 1.7 | 2 | 0.905 | 141 |
| 6 | 13 | 14.0 | 1.7 | 3 | 0.900 | 164 |
| 7 | 13 | 14.5 | 1.2 | 1 | 0.910 | 30 |
| 8 | 13 | 14.5 | 1.2 | 2 | 0.906 | 33 |
| 9 | 13 | 14.5 | 1.2 | 3 | 0.916 | 40 |
| 10 | 13 | 14.5 | 1.7 | 1 | 0.900 | 56 |
| 11 | 13 | 14.5 | 1.7 | 2 | 0.901 | 63 |
| 12 | 13 | 14.5 | 1.7 | 3 | 0.908 | 76 |
| 13 | 13 | 15.0 | 1.2 | 1 | 0.913 | 18 |
| 14 | 13 | 15.0 | 1.2 | 2 | 0.927 | 21 |
| 15 | 13 | 15.0 | 1.2 | 3 | 0.922 | 24 |
| 16 | 13 | 15.0 | 1.7 | 1 | 0.914 | 34 |
| 17 | 13 | 15.0 | 1.7 | 2 | 0.921 | 39 |
| 18 | 13 | 15.0 | 1.7 | 3 | 0.910 | 44 |
The interpretation is that in the best-case scenario (large mean difference of 2, small standard deviation of 1.2, and balanced design), a sample size of  (
( ) patients is sufficient to achieve a power of at least 0.9. In the worst-case scenario (small mean difference of 1, large standard deviation of 1.7, and a 1:3 unbalanced design), a sample size of
) patients is sufficient to achieve a power of at least 0.9. In the worst-case scenario (small mean difference of 1, large standard deviation of 1.7, and a 1:3 unbalanced design), a sample size of 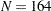 (
(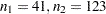 ) patients is necessary. The Nominal Power of 0.9 in the "Fixed Scenario Elements" table represents the input target power, and the Actual Power column in the "Computed N Total" table is the power at the sample size (N Total) adjusted to achieve the specified sample weighting exactly.
) patients is necessary. The Nominal Power of 0.9 in the "Fixed Scenario Elements" table represents the input target power, and the Actual Power column in the "Computed N Total" table is the power at the sample size (N Total) adjusted to achieve the specified sample weighting exactly.
Note the following characteristics of the analysis, and ways you can modify them if you want:
The total sample sizes are rounded up to multiples of the weight sums (2 for the 1:1 design, 3 for the 1:2 design, and 4 for the 1:3 design) to ensure that each group size is an integer. To request raw fractional sample size solutions, use the NFRACTIONAL option.
Only the group weight that varies (the one for group 2) is displayed as an output column, while the weight for group 1 appears in the "Fixed Scenario Elements" table. To display the group weights together in output columns, use the matched version of the value list rather than the crossed version.
If you can specify only differences between group means (instead of their individual values), or if you want to display the mean differences instead of the individual means, use the MEANDIFF= option instead of the GROUPMEANS= option.
The following statements implement all of these modifications:
proc power;
twosamplemeans
nfractional
meandiff = 1 to 2 by 0.5
stddev = 1.2 1.7
groupweights = (1 1) (1 2) (1 3)
power = 0.9
ntotal = .;
run;
Figure 68.5 shows the new results.
| Fixed Scenario Elements | |
|---|---|
| Distribution | Normal |
| Method | Exact |
| Nominal Power | 0.9 |
| Number of Sides | 2 |
| Null Difference | 0 |
| Alpha | 0.05 |
| Computed Ceiling N Total | |||||||
|---|---|---|---|---|---|---|---|
| Index | Mean Diff | Std Dev | Weight1 | Weight2 | Fractional N Total | Actual Power | Ceiling N Total |
| 1 | 1.0 | 1.2 | 1 | 1 | 62.507429 | 0.902 | 63 |
| 2 | 1.0 | 1.2 | 1 | 2 | 70.065711 | 0.904 | 71 |
| 3 | 1.0 | 1.2 | 1 | 3 | 82.665772 | 0.901 | 83 |
| 4 | 1.0 | 1.7 | 1 | 1 | 123.418482 | 0.901 | 124 |
| 5 | 1.0 | 1.7 | 1 | 2 | 138.598159 | 0.901 | 139 |
| 6 | 1.0 | 1.7 | 1 | 3 | 163.899094 | 0.900 | 164 |
| 7 | 1.5 | 1.2 | 1 | 1 | 28.961958 | 0.900 | 29 |
| 8 | 1.5 | 1.2 | 1 | 2 | 32.308867 | 0.906 | 33 |
| 9 | 1.5 | 1.2 | 1 | 3 | 37.893351 | 0.901 | 38 |
| 10 | 1.5 | 1.7 | 1 | 1 | 55.977156 | 0.900 | 56 |
| 11 | 1.5 | 1.7 | 1 | 2 | 62.717357 | 0.901 | 63 |
| 12 | 1.5 | 1.7 | 1 | 3 | 73.954291 | 0.900 | 74 |
| 13 | 2.0 | 1.2 | 1 | 1 | 17.298518 | 0.913 | 18 |
| 14 | 2.0 | 1.2 | 1 | 2 | 19.163836 | 0.913 | 20 |
| 15 | 2.0 | 1.2 | 1 | 3 | 22.282926 | 0.910 | 23 |
| 16 | 2.0 | 1.7 | 1 | 1 | 32.413512 | 0.905 | 33 |
| 17 | 2.0 | 1.7 | 1 | 2 | 36.195531 | 0.907 | 37 |
| 18 | 2.0 | 1.7 | 1 | 3 | 42.504535 | 0.903 | 43 |
Note that the Nominal Power of 0.9 applies to the raw computed sample size (Fractional N Total), and the Actual Power column applies to the rounded sample size (Ceiling N Total). Some of the adjusted sample sizes in Figure 68.5 are lower than those in Figure 68.4 because underlying group sample sizes are allowed to be fractional (for example, the first Ceiling N Total of 63 corresponding to equal group sizes of 31.5).
Copyright © SAS Institute, Inc. All Rights Reserved.