PROC PHREG uses the partial likelihood of the Cox model as the likelihood and generates a chain of posterior distribution samples by the Gibbs Sampler. Summary statistics, convergence diagnostics, and diagnostic plots are provided for each parameter. The following statements generate Figure 64.4–Figure 64.10:

ods graphics on;
proc phreg data=Rats;
   model Days*Status(0)=Group;
   bayes seed=1 outpost=Post;
run;
ods graphics off;

The BAYES statement invokes the Bayesian analysis. The SEED= option is specified to maintain reproducibility; the OUTPOST= option saves the posterior distribution samples in a SAS data set for postprocessiong; no other options are specified in the BAYES statement. By default, a uniform prior distribution is assumed on the regression coefficient Group. The uniform prior is a flat prior on the real line with a distribution that reflects ignorance of the location of the parameter, placing equal probability on all possible values the regression coefficient can take. Using the uniform prior in the following example, you would expect the Bayesian estimates to resemble the classical results of maximizing the likelihood. If you can elicit an informative prior on the regression coefficients, you should use the COEFFPRIOR= option to specify it.

You should make sure that the posterior distribution samples have achieved convergence before using them for Bayesian inference. PROC PHREG produces three convergence diagnostics by default. If you enable ODS Graphics before calling PROC PHREG as in the preceding program, diagnostics plots are also displayed.

The results of this analysis are shown in the following figures.

The "Model Information" table in Figure 64.4 summarizes information about the model you fit and the size of the simulation.

PROC PHREG first fits the Cox model by maximizing the partial likelihood. The only parameter in the model is the regression coefficient of Group. The maximum likelihood estimate (MLE) of the parameter and its 95% confidence interval are shown in Figure 64.5.

Since no prior is specified for the regression coefficient, the default uniform prior is used. This information is displayed in the "Uniform Prior for Regression Coefficients" table in Figure 64.6.

The "Fit Statistics" table in Figure 64.7 lists information about the fitted model. The table displays the DIC (deviance information criterion) and pD (effective number of parameters). See the section Fit Statistics for details.

Summary statistics of the posterior samples are displayed in the "Posterior Summaries" table and "Posterior Intervals" table as shown in Figure 64.8. Note that the mean and standard deviation of the posterior samples are comparable to the MLE and its standard error, respectively, due to the use of the uniform prior.

PROC PHREG provides diagnostics to assess the convergence of the generated Markov chain. Figure 64.9 shows three of these diagnostics: the lag1, lag5, lag10, and lag50 autocorrelations; the Geweke diagnostic; and the effective sample size. There is no indication that the Markov chain has not reached convergence. Refer to the section Statistical Diagnostic Tests for information about interpreting these diagnostics.

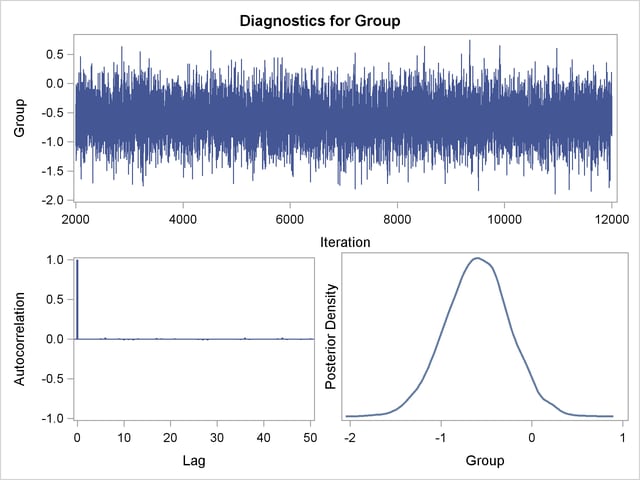
You can also assess the convergence of the generated Markov chain by examining the trace plot, the autocorrelation function plot, and the posterior density plot. Figure 64.10 displays a panel of these three plots for the parameter Group. This graphical display is automatically produced when ODS Graphics is enabled. Note that the trace of the samples centers on –0.6 with only small fluctuations, the autocorrelations are quite small, and the posterior density appears bell-shaped—all exemplifying the behavior of a converged Markov chain.

Figure 64.10 Diagnostic Plots

The proportional hazards model for comparing the two pretreatment groups is

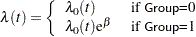The probability that the hazard of Group=0 is greater than that of Group=1 is

This probability can be enumerated from the posterior distribution samples by computing the fraction of samples with a coefficient less than 0. The following DATA step and PROC MEANS perform this calculation:

data New;
   set Post;
   Indicator=(Group < 0);
   label Indicator='Group < 0';
   run;
proc means data=New(keep=Indicator) n mean;
   run;

The PROC MEANS results are displayed in Figure 64.11. There is a 95.8% chance that the hazard rate of Group=0 is greater than that of Group=1. The result is consistent with the fact that the average survival time of Group=0 is less than that of Group=1.