| The MIXED Procedure |
Example 56.9 Examining Individual Test Components
The LCOMPONENTS option in the MODEL statement enables you to perform single-degree-of-freedom tests for individual rows of the 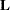 matrix. Such tests are useful to identify interaction patterns. In a balanced layout, Type 3 components of
matrix. Such tests are useful to identify interaction patterns. In a balanced layout, Type 3 components of 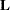 associated with A*B interactions correspond to simple contrasts of cell mean differences.
associated with A*B interactions correspond to simple contrasts of cell mean differences.
The first example revisits the data from the split-plot design by Stroup (1989a) that was analyzed in Example 56.1. Recall that variables A and B in the following statements represent the whole-plot and subplot factors, respectively:
proc mixed data=sp; class a b block; model y = a b a*b / LComponents e3; random block a*block; run;
The MIXED procedure constructs a separate 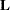 matrix for each of the three fixed-effects components. The matrices are displayed in Output 56.9.1. The tests for fixed effects are shown in Output 56.9.2.
matrix for each of the three fixed-effects components. The matrices are displayed in Output 56.9.1. The tests for fixed effects are shown in Output 56.9.2.
| Type 3 Coefficients for A | ||||
|---|---|---|---|---|
| Effect | A | B | Row1 | Row2 |
| Intercept | ||||
| A | 1 | 1 | ||
| A | 2 | 1 | ||
| A | 3 | -1 | -1 | |
| B | 1 | |||
| B | 2 | |||
| A*B | 1 | 1 | 0.5 | |
| A*B | 1 | 2 | 0.5 | |
| A*B | 2 | 1 | 0.5 | |
| A*B | 2 | 2 | 0.5 | |
| A*B | 3 | 1 | -0.5 | -0.5 |
| A*B | 3 | 2 | -0.5 | -0.5 |
If 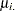 denotes a whole-plot main effect mean,
denotes a whole-plot main effect mean, 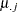 denotes a subplot main effect mean, and
denotes a subplot main effect mean, and  denotes a cell mean, the five components shown in Output 56.9.3 correspond to tests of the following:
denotes a cell mean, the five components shown in Output 56.9.3 correspond to tests of the following:
The first three components are comparisons of marginal means. The fourth component compares the effect of factor B at the first whole-plot level against the effect of B at the third whole-plot level. Finally, the last component tests whether the factor B effect changes between the second and third whole-plot level.
The Type 3 component tests can also be produced with these corresponding ESTIMATE statements:
proc mixed data=sp; class a b block ; model y = a b a*b; random block a*block; estimate 'a 1' a 1 0 -1; estimate 'a 2' a 0 1 -1; estimate 'b 1' b 1 -1; estimate 'a*b 1' a*b 1 -1 0 0 -1 1; estimate 'a*b 2' a*b 0 0 1 -1 -1 1; ods select Estimates; run;
The results are shown in Output 56.9.4.
A second useful application of the LCOMPONENTS option is in polynomial models, where Type 1 tests are often used to test the entry of model terms sequentially. The SOLUTION option in the MODEL statement displays the regression coefficients that correspond to a Type 3 analysis. That is, the coefficients represent the partial coefficients you would get by adding the regressor variable last in a model containing all other effects, and the tests are identical to those in the "Type 3 Tests of Fixed Effects" table.
Consider the following DATA step and the fit of a third-order polynomial regression model.
data polynomial; do x=1 to 20; input y@@; output; end; datalines; 1.092 1.758 1.997 3.154 3.880 3.810 4.921 4.573 6.029 6.032 6.291 7.151 7.154 6.469 7.137 6.374 5.860 4.866 4.155 2.711 ;
proc mixed data=polynomial; model y = x x*x x*x*x / s lcomponents htype=1,3; run;
The t tests displayed in the "Solution for Fixed Effects" table are Type 3 tests, sometimes referred to as partial tests. They measure the contribution of a regressor in the presence of all other regressor variables in the model.
The Type 3 L components are identical to the tests in the "Solutions for Fixed Effects" table shown in Output 56.9.5. The Type 1 table yields the following:
sequential (Type 1) tests of regression variables that test the significance of a regressor given all other variables preceding it in the model list
the regression coefficients for sequential submodels
The estimate of 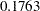 is the regression coefficient in a simple linear regression of Y on X. The estimate of
is the regression coefficient in a simple linear regression of Y on X. The estimate of  is the partial coefficient for the quadratic term when it is added to a model containing only a linear component. Similarly, the value
is the partial coefficient for the quadratic term when it is added to a model containing only a linear component. Similarly, the value 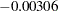 is the partial coefficient for the cubic term when it is added to a model containing a linear and quadratic component. The last Type 1 component is always identical to the corresponding Type 3 component.
is the partial coefficient for the cubic term when it is added to a model containing a linear and quadratic component. The last Type 1 component is always identical to the corresponding Type 3 component.
Copyright © SAS Institute, Inc. All Rights Reserved.