| The LOGISTIC Procedure |
Example 51.7 ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits
This example plots an ROC curve, estimates a customized odds ratio, produces the traditional goodness-of-fit analysis, displays the generalized 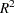 measures for the fitted model, calculates the normal confidence intervals for the regression parameters, and produces a display of the probability function and prediction curves for the fitted model. The data consist of three variables: n (number of subjects in the sample), disease (number of diseased subjects in the sample), and age (age for the sample). A linear logistic regression model is used to study the effect of age on the probability of contracting the disease. The statements to produce the data set and perform the analysis are as follows:
measures for the fitted model, calculates the normal confidence intervals for the regression parameters, and produces a display of the probability function and prediction curves for the fitted model. The data consist of three variables: n (number of subjects in the sample), disease (number of diseased subjects in the sample), and age (age for the sample). A linear logistic regression model is used to study the effect of age on the probability of contracting the disease. The statements to produce the data set and perform the analysis are as follows:
data Data1; input disease n age; datalines; 0 14 25 0 20 35 0 19 45 7 18 55 6 12 65 17 17 75 ;
ods graphics on;
proc logistic data=Data1 plots(only)=roc(id=obs);
model disease/n=age / scale=none
clparm=wald
clodds=pl
rsquare;
units age=10;
effectplot;
run;
ods graphics off;
The option SCALE=NONE is specified to produce the deviance and Pearson goodness-of-fit analysis without adjusting for overdispersion. The RSQUARE option is specified to produce generalized 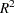 measures of the fitted model. The CLPARM=WALD option is specified to produce the Wald confidence intervals for the regression parameters. The UNITS statement is specified to produce customized odds ratio estimates for a change of 10 years in the age variable, and the CLODDS=PL option is specified to produce profile-likelihood confidence limits for the odds ratio. The ODS GRAPHICS ON statement and the PLOTS= option produce a graphical display of the ROC curve, and the EFFECTPLOT statement displays the model fit.
measures of the fitted model. The CLPARM=WALD option is specified to produce the Wald confidence intervals for the regression parameters. The UNITS statement is specified to produce customized odds ratio estimates for a change of 10 years in the age variable, and the CLODDS=PL option is specified to produce profile-likelihood confidence limits for the odds ratio. The ODS GRAPHICS ON statement and the PLOTS= option produce a graphical display of the ROC curve, and the EFFECTPLOT statement displays the model fit.
The results in Output 51.7.1 show that the deviance and Pearson statistics indicate no lack of fit in the model.
Output 51.7.2 shows that the R-square for the model is 0.74. The odds of an event increases by a factor of 7.9 for each 10-year increase in age.
| Model Fit Statistics | ||
|---|---|---|
| Criterion | Intercept Only |
Intercept and Covariates |
| AIC | 124.173 | 52.468 |
| SC | 126.778 | 57.678 |
| -2 Log L | 122.173 | 48.468 |
| Testing Global Null Hypothesis: BETA=0 | |||
|---|---|---|---|
| Test | Chi-Square | DF | Pr > ChiSq |
| Likelihood Ratio | 73.7048 | 1 | <.0001 |
| Score | 55.3274 | 1 | <.0001 |
| Wald | 23.3475 | 1 | <.0001 |
| Analysis of Maximum Likelihood Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
Wald Chi-Square |
Pr > ChiSq |
| Intercept | 1 | -12.5016 | 2.5555 | 23.9317 | <.0001 |
| age | 1 | 0.2066 | 0.0428 | 23.3475 | <.0001 |
| Association of Predicted Probabilities and Observed Responses |
|||
|---|---|---|---|
| Percent Concordant | 92.6 | Somers' D | 0.906 |
| Percent Discordant | 2.0 | Gamma | 0.958 |
| Percent Tied | 5.4 | Tau-a | 0.384 |
| Pairs | 2100 | c | 0.953 |
Since the ODS GRAPHICS ON statement is specified, a graphical display of the ROC curve is produced as shown in Output 51.7.3.
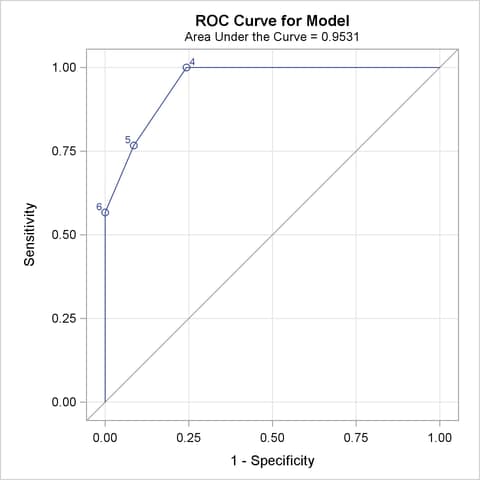
Note that the area under the ROC curve is estimated by the statistic c in the "Association of Predicted Probabilities and Observed Responses" table. In this example, the area under the ROC curve is 0.953.
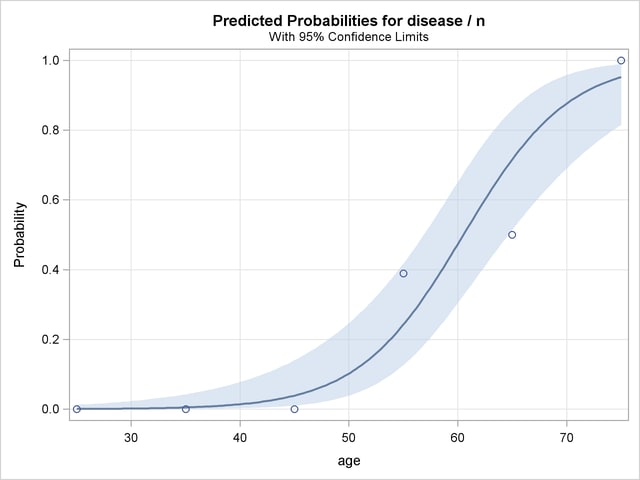
Because there is only one continuous covariate, the ODS GRAPHICS ON statement and the EFFECTPLOT statement produce a graphical display of the predicted probability curve with bounding 95% confidence limits as shown in Output 51.7.4.
Copyright © SAS Institute, Inc. All Rights Reserved.