| The GENMOD Procedure |
| Case Deletion Diagnostic Statistics |
For ordinary generalized linear models, regression diagnostic statistics developed by Williams (1987) can be requested in an output data set or in the OBSTATS table by specifying the DIAGNOSTICS | INFLUENCE option in the MODEL statement. These diagnostics measure the influence of an individual observation on model fit, and generalize the one-step diagnostics developed by Pregibon (1981) for the logistic regression model for binary data.
Preisser and Qaqish (1996) further generalized regression diagnostics to apply to models for correlated data fit by generalized estimating equations (GEEs), where the influence of entire clusters of correlated observations, or the influence of individual observations within a cluster, is measured. These diagnostic statistics can be requested in an output data set or in the OBSTATS table if a model for correlated data is specified with a REPEATED statement.
The next two sections use the following notation:
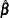
is the maximum likelihood estimate of the regression parameters
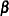 , or, in the case of correlated data, the solution of the GEEs.
, or, in the case of correlated data, the solution of the GEEs. 
is the corresponding estimate evaluated with the
 th observation deleted, or, in the case of correlated data, with the
th observation deleted, or, in the case of correlated data, with the  th cluster deleted.
th cluster deleted. 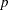
is the dimension of the regression parameter vector
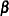 .
. 
is the standardized Pearson residual
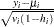 , where
, where  is the variance of the
is the variance of the  th response and
th response and 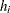 is the leverage defined in the section H | LEVERAGE.
is the leverage defined in the section H | LEVERAGE. 
is the variance of response
 ,
, 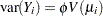 , where
, where  is the variance function and
is the variance function and 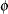 is the dispersion parameter.
is the dispersion parameter. 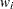
is the prior weight of the
 th observation specified with the WEIGHT statement. If there is no WEIGHT statement,
th observation specified with the WEIGHT statement. If there is no WEIGHT statement, 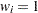 for all
for all  .
.
All unknown quantities are replaced by their estimated values in the following two sections.
Diagnostics for Ordinary Generalized Linear Models
The following statistics are available for generalized linear models.
DFBETA
The DFBETA statistic for measuring the influence of the  th observation is defined as the one-step approximation to the difference in the MLE of the regression parameter vector and the MLE of the regression parameter vector without the
th observation is defined as the one-step approximation to the difference in the MLE of the regression parameter vector and the MLE of the regression parameter vector without the  th observation. This one-step approximation assumes a Fisher scoring step, and is given by
th observation. This one-step approximation assumes a Fisher scoring step, and is given by
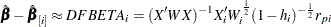 |
where 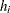 is the leverage defined in the section H | LEVERAGE.
is the leverage defined in the section H | LEVERAGE.
DFBETAS
The standardized DFBETA statistic for assessing the influence of the  th observation on the
th observation on the 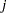 th regression parameter is defined as the DFBETA statistic for the
th regression parameter is defined as the DFBETA statistic for the 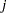 th parameter divided by its estimated standard deviation, where the standard deviation is estimated from all the data.
th parameter divided by its estimated standard deviation, where the standard deviation is estimated from all the data.
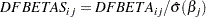 |
DOBS | COOKD | COOKSD
In normal linear regression, the influence of observation  can be measured by Cook’s distance (Cook and Weisberg; 1982). A measure of influence of observation
can be measured by Cook’s distance (Cook and Weisberg; 1982). A measure of influence of observation  for generalized linear models that is equivalent to Cook’s distance for normal linear regression is given by
for generalized linear models that is equivalent to Cook’s distance for normal linear regression is given by
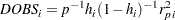 |
where 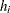 is the leverage defined in the section H | LEVERAGE. This measure is the one-step approximation to
is the leverage defined in the section H | LEVERAGE. This measure is the one-step approximation to 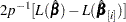 , where
, where 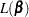 is the log likelihood evaluated at
is the log likelihood evaluated at 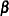 .
.
H | LEVERAGE
The Fisher scores, or expected, weight for observation  is
is 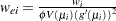 . Let
. Let  be the diagonal matrix with
be the diagonal matrix with 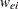 as the
as the  th diagonal. The leverage
th diagonal. The leverage 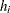 of the
of the  th observation is defined as the
th observation is defined as the  th diagonal element of the hat matrix
th diagonal element of the hat matrix
 |
Diagnostics for Models Fit by Generalized Estimating Equations (GEEs)
The diagnostic statistics in this section were developed by Preisser and Qaqish (1996). See the section Generalized Estimating Equations for further information and notation for generalized estimating equations (GEEs). The following additional notation is used in this section.
Partition the design matrix 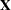 and response vector
and response vector 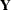 by cluster; that is, let
by cluster; that is, let 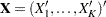 , and
, and 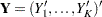 corresponding to the
corresponding to the 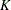 clusters.
clusters.
Let 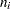 be the number of responses for cluster
be the number of responses for cluster  , and denote by
, and denote by 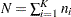 the total number of observations. Denote by
the total number of observations. Denote by 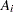 the
the 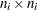 diagonal matrix with
diagonal matrix with 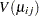 as the
as the 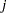 th diagonal element. If there is a WEIGHT statement, the diagonal element of
th diagonal element. If there is a WEIGHT statement, the diagonal element of 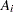 is
is 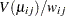 , where
, where 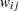 is the specified weight of the
is the specified weight of the 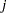 th observation in the
th observation in the  th cluster. Let
th cluster. Let 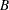 the
the  diagonal matrix with
diagonal matrix with 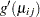 as diagonal elements,
as diagonal elements, 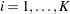 ,
, 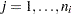 . Let
. Let  the
the 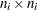 diagonal matrix corresponding to cluster
diagonal matrix corresponding to cluster  with
with 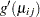 as the
as the 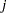 th diagonal element.
th diagonal element.
Let  be the
be the 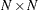 block diagonal weight matrix whose
block diagonal weight matrix whose  th block, corresponding to the
th block, corresponding to the  th cluster, is the
th cluster, is the 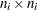 matrix
matrix
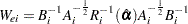 |
where 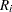 is the working correlation matrix for cluster
is the working correlation matrix for cluster  .
.
Let
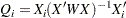 |
where 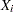 is the
is the 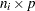 design matrix corresponding to cluster
design matrix corresponding to cluster  .
.
Define the adjusted residual vector as
 |
and  , the estimated residual for the
, the estimated residual for the  th cluster.
th cluster.
Let the subscript 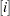 denote estimates evaluated without the
denote estimates evaluated without the  th cluster,
th cluster, 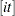 estimates evaluated using all the data except the
estimates evaluated using all the data except the  th observation of the
th observation of the  th cluster, and let
th cluster, and let 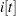 denote matrices corresponding to the
denote matrices corresponding to the  th cluster without the
th cluster without the  th observation.
th observation.
The following statistics are available for generalized estimating equation models.
CH | CLUSTERH | CLEVERAGE
The leverage of cluster  is contained in the matrix
is contained in the matrix 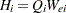 , and is summarized by the trace of
, and is summarized by the trace of  ,
,
 |
The leverage 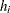 of the
of the  th observation in the
th observation in the  th cluster is the
th cluster is the  th diagonal element of
th diagonal element of  .
.
DFBETAC
The effect of deleting cluster  on the estimated parameter vector is given by the following one-step approximation for
on the estimated parameter vector is given by the following one-step approximation for  :
:
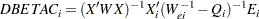 |
DFBETACS
The cluster deletion statistic DFBETAC can be standardized using the variances of 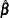 based on the complete data. The standardized one-step approximation for the change in
based on the complete data. The standardized one-step approximation for the change in  due to deletion of cluster
due to deletion of cluster  is
is
 |
DFBETAO
Partition the matrices 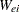 and
and 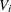 as
as
 |
 |
and let  and
and 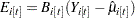 .
.
The effect of deleting the  th observation from the
th observation from the  th cluster is given by the following one-step approximation to
th cluster is given by the following one-step approximation to  :
:
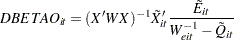 |
where 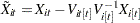 ,
, 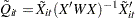 , and
, and  . Note that
. Note that 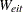 ,
, 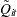 , and
, and  are scalars.
are scalars.
DFBETAOS
The observation deletion statistic DFBETAO can be standardized using the variances of 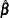 based on the complete data. The standardized one-step approximation for the change in
based on the complete data. The standardized one-step approximation for the change in  due to deletion of observation
due to deletion of observation  in cluster
in cluster  is
is
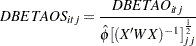 |
DCLS | CLUSTERCOOKD | CLUSTERCOOKSD
A measure of the standardized influence of the subset  of observations on the overall fit is
of observations on the overall fit is  . For deletion of cluster
. For deletion of cluster  , this is approximated by
, this is approximated by
 |
DOBS | COOKD | COOKSD
The measure of overall fit in the section DCLS | CLUSTERCOOKD | CLUSTERCOOKSD for the deletion of the  th observation in the
th observation in the  th cluster is approximated by
th cluster is approximated by
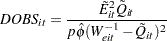 |
where  ,
, 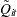 , and
, and 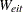 are defined in the section DFBETAO. In the case of the independence working correlation, this is equal to the measure for ordinary generalized linear models defined in the section DOBS | COOKD | COOKSD.
are defined in the section DFBETAO. In the case of the independence working correlation, this is equal to the measure for ordinary generalized linear models defined in the section DOBS | COOKD | COOKSD.
MCLS | CLUSTERDFIT
A studentized distance measure of the type defined in the section DCLS | CLUSTERCOOKD | CLUSTERCOOKSD of the influence of the  th cluster is given by
th cluster is given by
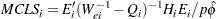 |
Copyright © SAS Institute, Inc. All Rights Reserved.