| The CALIS Procedure |
Example 25.16 Simultaneous Equations with Mean Structures and Reciprocal Paths
The supply-and-demand food example of Kmenta (1971, pp. 565, 582) is used to illustrate PROC CALIS for the estimation of intercepts and coefficients of simultaneous equations in econometrics. The model is specified by two simultaneous equations containing two endogenous variables 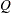 and
and 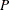 , and three exogenous variables
, and three exogenous variables  ,
, 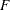 , and
, and  :
:
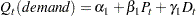 |
 |
for  , ...,
, ..., 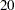 .
.
To analyze this model in PROC CALIS, the second equation needs to be written in another form. For instance, in the LINEQS model each endogenous variable must appear on the left-hand side of exactly one equation. To satisfy this requirement, you can rewrite the second equation as an equation for  as:
as:
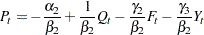 |
or, equivalently reparameterized as:
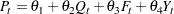 |
where
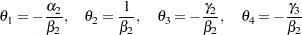 |
This new equation for  together with the first equation for
together with the first equation for 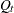 suggest the following LINEQS model specification in PROC CALIS:
suggest the following LINEQS model specification in PROC CALIS:
title 'Food example of KMENTA(1971, p.565 & 582)';
data food;
input Q P D F Y;
label Q='Food Consumption per Head'
P='Ratio of Food Prices to General Price'
D='Disposable Income in Constant Prices'
F='Ratio of Preceding Years Prices'
Y='Time in Years 1922-1941';
datalines;
98.485 100.323 87.4 98.0 1
99.187 104.264 97.6 99.1 2
102.163 103.435 96.7 99.1 3
101.504 104.506 98.2 98.1 4
104.240 98.001 99.8 110.8 5
103.243 99.456 100.5 108.2 6
103.993 101.066 103.2 105.6 7
99.900 104.763 107.8 109.8 8
100.350 96.446 96.6 108.7 9
102.820 91.228 88.9 100.6 10
95.435 93.085 75.1 81.0 11
92.424 98.801 76.9 68.6 12
94.535 102.908 84.6 70.9 13
98.757 98.756 90.6 81.4 14
105.797 95.119 103.1 102.3 15
100.225 98.451 105.1 105.0 16
103.522 86.498 96.4 110.5 17
99.929 104.016 104.4 92.5 18
105.223 105.769 110.7 89.3 19
106.232 113.490 127.1 93.0 20
;
proc calis data=food pshort nostand;
lineqs
Q = alpha1 * Intercept + beta1 * P + gamma1 * D + E1,
P = theta1 * Intercept + theta2 * Q + theta3 * F + theta4 * Y + E2;
variance
E1-E2 = eps1-eps2;
cov
E1-E2 = eps3;
bounds
eps1-eps2 >= 0. ;
run;
The LINEQS modeling language is used in this example because its specification is similar to the original equations. In the LINEQS statement, you essentially input the two model equations for Q and P. Parameters for intercepts and regression coefficients are also specified in the equations. Note that Intercept in the two equations is treated as a special variable that contains ones for all observations. Intercept is not a variable in the data set, nor do you need to create such a variable in your data set. Hence, the variable Intercept does not represent the intercept parameter itself. Instead, the intercept parameters for the two equations are the coefficients attached to Intercept. In this example, the intercept parameters are alpha1 and theta1, respectively, in the two equations. As required, error terms E1 and E2 are added to complete the equation specification.
In the VARIANCE statement, you specify eps1 and eps2, respectively, for the variance parameters of the error terms. In the COV, you specify eps3 for the covariance parameter between the error terms. In the BOUNDS statement, you set lower bounds for the error variances so that estimates of eps1 and eps2 would be nonnegative.
In this example, the PSHORT and the NOSTAND options are used in the PROC CALIS statement. The PSHORT option suppresses a large amount of the output. For example, initial estimates are not printed and simple descriptive statistics and standard errors are not computed. The NOSTAND option suppresses the printing of the standardized results. Because the default printing in PROC CALIS might produce a large amount of output, using these printing options make your output more concise and readable. Whenever appropriate, you may consider using these printing options.
The estimated equations are shown in Output 25.16.1.
| Linear Equations | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q | = | 93.6193 | * | Intercept | + | -0.2295 | * | P | + | 0.3100 | * | D | + | 1.0000 | E1 | ||||||
| Std Err | 7.5748 | alpha1 | 0.0923 | beta1 | 0.0448 | gamma1 | |||||||||||||||
| t Value | 12.3592 | -2.4856 | 6.9186 | ||||||||||||||||||
| P | = | -218.9 | * | Intercept | + | 4.2140 | * | Q | + | -0.9305 | * | F | + | -1.5579 | * | Y | + | 1.0000 | E2 | ||
| Std Err | 137.7 | theta1 | 1.7540 | theta2 | 0.3960 | theta3 | 0.6650 | theta4 | |||||||||||||
| t Value | -1.5897 | 2.4025 | -2.3500 | -2.3429 | |||||||||||||||||
The estimates of intercepts and regression coefficients are shown directly in the equations. Any number in an equation followed by an asterisk is an estimate. For the estimates in equations, the parameter names are shown underneath the associated variables. Any number in an equation not followed by an asterisk is a fixed value. For example, the value 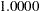 attached to the error term in each of the output equation is fixed. Also, for fixed coefficients there are no parameter names underneath the associated variables.
attached to the error term in each of the output equation is fixed. Also, for fixed coefficients there are no parameter names underneath the associated variables.
All but the intercept estimates in the equation for predicting P are statistically significant at 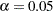 (when using an approximate critical value of 2). The
(when using an approximate critical value of 2). The  ratio for theta1 is
ratio for theta1 is  , which implies that this intercept might have been zero in the population. However, because you have reparameterized the original model to use the LINEQS model specification, transformed parameters like theta1 in this model might not be of primary interest. Therefore, you might not need to pay any attention to the significance of the theta1 estimate. There is a way to use the original econometric parameters to specify the LINEQS model. It is discussed in the later part of this example.
, which implies that this intercept might have been zero in the population. However, because you have reparameterized the original model to use the LINEQS model specification, transformed parameters like theta1 in this model might not be of primary interest. Therefore, you might not need to pay any attention to the significance of the theta1 estimate. There is a way to use the original econometric parameters to specify the LINEQS model. It is discussed in the later part of this example.
Estimates for variance, covariance, and mean parameters are shown in Output 25.16.2.
| Estimates for Variances of Exogenous Variables | |||||
|---|---|---|---|---|---|
| Variable Type |
Variable | Parameter | Estimate | Standard Error |
t Value |
| Error | E1 | eps1 | 3.51274 | 1.20204 | 2.92233 |
| E2 | eps2 | 105.06749 | 83.89446 | 1.25238 | |
| Observed | D | _Add1 | 139.96029 | 45.40911 | 3.08221 |
| F | _Add2 | 161.51355 | 52.40192 | 3.08221 | |
| Y | _Add3 | 35.00000 | 11.35550 | 3.08221 | |
Parameters with a name prefix _Add are added automatically by PROC CALIS. These parameters are added as free parameters to complete the model specification. In PROC CALIS, variances and covariances among the set of exogenous manifest variables must be parameters. You either specify them explicitly or let the CALIS procedure to add them. If you need to constrain or to fix these parameters, then you must specify them explicitly. When your model also fits the mean structures, the same principle applies to the means of the exogenous manifest variables. In this example, because variables D, F, and Y are all exogenous manifest variables, their associated means, variances and covariances must be parameters in the model.
The squared multiple correlations for the equations are shown in Output 25.16.3.
For endogenous variable P, the R-square is 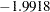 , which is obviously an invalid value. In fact, because there are correlated errors (between E1 and E2) and reciprocal paths (paths to and from Q and P), the model departs from the regular assumptions of multiple regression analysis. As a result, you should not interpret the R-squares for this example.
, which is obviously an invalid value. In fact, because there are correlated errors (between E1 and E2) and reciprocal paths (paths to and from Q and P), the model departs from the regular assumptions of multiple regression analysis. As a result, you should not interpret the R-squares for this example.
Specifying the LINEQS with the Original Econometric Parameters
If you are interested in estimating the parameters in the original econometric model (that is, 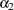 ,
, 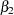 ,
, 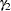 , and
, and 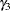 ), the previous reparameterized LINEQS model does not serve your purpose well enough. However, using the relations between these original parameters with the
), the previous reparameterized LINEQS model does not serve your purpose well enough. However, using the relations between these original parameters with the 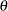 parameters in the reparameterized LINEQS model, you can set up some "super-parameters" in the LINEQS model, as shown in the following statements:
parameters in the reparameterized LINEQS model, you can set up some "super-parameters" in the LINEQS model, as shown in the following statements:
proc calis data=Food pshort nostand;
lineqs
Q = alpha1 * Intercept + beta1 * P + gamma1 * D + E1,
P = theta1 * Intercept + theta2 * Q + theta3 * F + theta4 * Y + E2;
variance
E1-E2 = eps1-eps2;
cov
E1-E2 = eps3;
bounds
eps1-eps2 >= 0. ;
parameters alpha2 (50.) beta2 gamma2 gamma3 (3*.25);
theta1 = -alpha2 / beta2;
theta2 = 1 / beta2;
theta3 = -gamma2 / beta2;
theta4 = -gamma3 / beta2;
run;
In this new specification, only the PARAMETERS statement and the SAS programming statements following it are new. In the PARAMETERS statement, you define super-parameters alpha2, beta2, gamma2, and gamma3, and put initial values for them in parentheses. These parameters are the original econometric parameters of interest. The SAS programming statements that follow the PARAMETERS statement are used to define the functional relationships of the super-parameters with the parameters in the LINEQS model. Consequently, in this new specification, theta1, theta2, theta3, and theta4 are no longer independent parameters in the model, as they are in the previous reparameterized model. Instead, alpha2, beta2, gamma2, and gamma3 are independent parameters in this new specification. By fitting this new model, you get the same set of estimates as those in the previous LINEQS model. In addition, you get estimates of the super-parameters, as shown in Output 25.16.4.
You can now interpret the results in terms of the original econometric parameterization. As shown in Output 25.16.4, all these estimates are significant, despite the fact that one of the transformed parameter estimates in the linear equations of the LINEQS model is not. You can obtain almost equivalent results by applying the SAS/ETS procedure SYSLIN on this problem.
Alternative Ways to Specify Your LINEQS Model
In specifying the linear equations in the LINEQS model, it might become cumbersome when you need to name a lot of parameters into the equations. If the parameters in your model are unconstrained, you need to very careful to use unique parameter names to distinguish the free parameters because parameters with the same name are identical and will have the same estimate. To make model specification easier and to avoid accidental constraints, PROC CALIS provides an efficient way to specify these free parameters. That is, you can simply omit the parameter names in the specification. For example, in the first specification of the current example, except for the boundary constraints on the error variance parameters, all other parameters in the model are not constrained, as shown in the following statements:
proc calis data=food pshort nostand;
lineqs
Q = alpha1 * Intercept + beta1 * P + gamma1 * D + E1,
P = theta1 * Intercept + theta2 * Q + theta3 * F + theta4 * Y + E2;
variance
E1-E2 = eps1-eps2;
cov
E1-E2 = eps3;
bounds
eps1-eps2 >= 0. ;
run;
Parameters such as alpha1, beta1, and so on are unique parameter names in the specific locations of the model. They are free parameters. Hence, you can use the following equivalent specification:
proc calis data=food pshort nostand;
lineqs
Q = * Intercept + * P + * D + E1,
P = * Intercept + * Q + * F + * Y + E2;
variance
E1-E2 = eps1-eps2;
cov
E1 E2;
bounds
eps1-eps2 >= 0. ;
run;
Only the parameters eps1 and eps2 remain in this equivalent specification. You omit the specification of all other parameter names. But the estimation results are the same, as shown in Output 25.16.5.
| Linear Equations | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q | = | 93.6193 | * | Intercept | + | -0.2295 | * | P | + | 0.3100 | * | D | + | 1.0000 | E1 | ||||||
| Std Err | 7.5748 | _Parm1 | 0.0923 | _Parm2 | 0.0448 | _Parm3 | |||||||||||||||
| t Value | 12.3592 | -2.4856 | 6.9186 | ||||||||||||||||||
| P | = | -218.9 | * | Intercept | + | 4.2140 | * | Q | + | -0.9305 | * | F | + | -1.5579 | * | Y | + | 1.0000 | E2 | ||
| Std Err | 137.7 | _Parm4 | 1.7540 | _Parm5 | 0.3960 | _Parm6 | 0.6650 | _Parm7 | |||||||||||||
| t Value | -1.5897 | 2.4025 | -2.3500 | -2.3429 | |||||||||||||||||
| Estimates for Variances of Exogenous Variables | |||||
|---|---|---|---|---|---|
| Variable Type |
Variable | Parameter | Estimate | Standard Error |
t Value |
| Error | E1 | eps1 | 3.51274 | 1.20204 | 2.92233 |
| E2 | eps2 | 105.06749 | 83.89446 | 1.25238 | |
| Observed | D | _Add1 | 139.96029 | 45.40911 | 3.08221 |
| F | _Add2 | 161.51355 | 52.40192 | 3.08221 | |
| Y | _Add3 | 35.00000 | 11.35550 | 3.08221 | |
The estimation results in Output 25.16.5 are the same as those in Output 25.16.2 and Output 25.16.3 with the original LINEQS model specification, only now PROC CALIS generates the parameter names with the _Parm in the results, as shown in Output 25.16.5. Note that you retain the parameter names eps1 and eps2 because you need to refer to them in the BOUNDS statement.
Copyright © SAS Institute, Inc. All Rights Reserved.