| The CALIS Procedure |
| MATRIX Statement |
MATRIX statement specifies the matrix elements (locations) and their parameters. Parameters can be fixed or free, with or without initial estimates. The matrix-name indicates the matrix to specify in the MATRIX statement. The location indicates the starting row and column numbers of the matrix being specified and the parameter-spec is a list of free or fixed parameters for the elements that are indicated by the location.
The MATRIX statement is a subsidiary model specification statement of the COSAN, LISMOD, and MSTRUCT modeling languages. You might need to use the MATRIX statements as many times as needed for specifying your model. However, you can use the MATRIX statement at most once for each distinct model matrix.
Valid Matrix Names for the COSAN Model
The valid matrix-names depend on the your specification in the COSAN statement in which you define the COSAN model matrices and their properties. Except for those fixed matrices with the IDE or ZID type, you can use the MATRIX statement to specify any COSAN model matrices you define in the COSAN statement.
Valid Matrix Names for the LISMOD Model
There are 12 model matrices in the LISMOD model, and they correspond to the following valid matrix-names :
matrices and their types in the measurement model for the
 -variables
-variables - _LAMBDAY_
the matrix of regression coefficients of the
 -variables on the
-variables on the 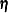 -variables (general, GEN)
-variables (general, GEN) - _NUY_
the vector of intercept terms of the
 -variables (general, GEN)
-variables (general, GEN) - _THETAY_
the error covariance matrix for the
 -variables (symmetric, SYM)
-variables (symmetric, SYM)
matrices and their types in the measurement model for the
 -variables
-variables - _LAMBDAX_
the matrix of regression coefficients of the
 -variables on the
-variables on the 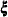 -variables (general, GEN)
-variables (general, GEN) - _NUX_
the vector of intercept terms of the
 -variables (general, GEN)
-variables (general, GEN) - _THETAX_
the error covariance matrix for the
 -variables (symmetric, SYM)
-variables (symmetric, SYM)
matrices and their types in the structural model
- _ALPHA_
the vector of intercept terms of the
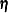 -variables (general, GEN)
-variables (general, GEN) - _BETA_
the matrix of regression coefficients of the
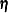 -variables on the
-variables on the 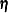 -variables (general, GEN)
-variables (general, GEN) - _GAMMA_
the matrix of regression coefficients of the
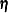 -variables on the
-variables on the 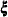 -variables (general, GEN)
-variables (general, GEN) - _KAPPA_
the mean vector for the
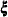 -variables (general, GEN)
-variables (general, GEN) - _PHI_
the covariance matrix for the
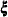 -variables (symmetric, SYM)
-variables (symmetric, SYM) - _PSI_
the error covariance matrix for the
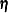 -variables (symmetric, SYM)
-variables (symmetric, SYM)
Valid Matrix Names for the MSTRUCT Modeling Language
The following matrix-names are valid for the MSTRUCT modeling language:
- _COV_
the covariance matrix (symmetric, SYM)
- _MEAN_
the mean vector (general, GEN)
Specifying Locations in Model Matrices
The five main types of matrix locations (elements) specification in the MATRIX statement are briefly described in the following:
Unspecified location: Blank or [ , ]
Use this notation to specify the [1,1] element of the matrix, and to specify the remaining valid elements of the matrix in a prescribed order until all the parameters in the parameter-spec list are assigned.Row-and-column location: [i,j], [@i,j], [i,@j], or [@i,@j]
Use this notation to specify the [i,j] element of a matrix, and to specify the remaining elements of the matrix in the order indicated by the location notation until all the parameters in the parameter-spec list are assigned.Row location only: [i,], [@i,], or [iset,]
Use this notation to specify the first valid matrix element in the [i]-th row (for the first two notations) or the [i1]-th row (for the [iset,] notation, where iset=(i1, i2, ...) is a set of row numbers), and to specify the remaining elements of the matrix in the order indicated by the location notation until all the parameters in the parameter-spec list are assigned.Column location only: [,j], [,@j], or [,jset]
Use this notation to specify the first valid matrix element in the [j]-th column (for the first two notations) or the [j1]-th column (for the [,jset] notation, where jset=(j1, j2, ...) is a set of columns), and to specify the remaining elements of the matrix in the order indicated by the location notation until all the parameters in the parameter-spec list are assigned.Row-and-column-sets location: [iset,jset], [iset,j], or [i,jset]
Use this notation to specify the [i1,j1] element of the matrix, where i1 is either the same as i or the first row number specified in iset, and j1 is either the same as j or the first column number specified in jset, and to specify the remaining elements of the matrix in the order indicated by the location notation until all the parameters in the parameter-spec list are assigned.
Consider the following points about the location specifications:
In the description of the various location specifications, the starting matrix element for parameter assignment is relatively well-defined. However, if the parameter-spec list has more than one parameter, there are more matrix elements to assign with the parameters in the parameter-spec list. If there is no parameter-spec list, a set of matrix elements are specified as unnamed free parameters. Hence, the actual number of elements specified by these location specifications depends on the length of the parameter-spec list.
Because more than one matrix element could be specified in any of these location specifications, it is important to understand the order that PROC CALIS uses to assign the matrix elements.
In some of the location specifications, either the row or column is unspecified and the assignment of the matrix element starts with the first valid element given the column or the row number. This first valid element depends on the type of the matrix in question.
The next few sections describe the parameter assignments in more detail for each of these location specifications in the MATRIX statement.
Unspecified Location: Blank or [ , ]
This notation means that all valid elements started with the [1,1] element of the matrix specified in the model. If no parameter-spec list is specified, all valid elements in the matrix are unnamed free parameters. For these elements, PROC CALIS generates parameter names with the _Parm prefix followed by a unique integer (for example, _Parm1, _Parm2, and so on). If a parameter-spec list is specified, the assignment of parameters starts with the [1,1] element and proceeds to the next valid elements in the same row. If the entire row of valid elements is assigned with parameters, it proceeds to the next row and so on, until all the parameters in the parameter-spec list are assigned. The valid element given the row or column number depends on the type of matrix in question. The following examples illustrate the usage of the unspecified location notation.
Suppose that _GAMMA_ is a general 3  3 matrix. The following statement specifies four elements of this matrix:
3 matrix. The following statement specifies four elements of this matrix:
matrix _GAMMA_ [,] = gg1-gg4;
Equivalently, you can use the following blank location specification:
matrix _GAMMA_ = gg1-gg4;
Both specifications are equivalent to the following elementwise specification:
matrix _GAMMA_ [1,1] = gg1,
[1,2] = gg2,
[1,3] = gg3,
[2,1] = gg4;
With the unspecified location for the matrix _GAMMA_, the first row is filled up with the parameters first. Then it proceeds to the next row and so on until all parameters in the parameter-spec list are assigned. Because there are four parameters and _GAMMA_ has three columns, the parameter gg4 is assigned to the _GAMMA_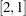 element.
element.
However, if the preceding specification is for a 3  3 matrix symmetric matrix _PHI_, the parameters are assigned differently. That is, the following specification has different matrix elements assigned with the parameters:
3 matrix symmetric matrix _PHI_, the parameters are assigned differently. That is, the following specification has different matrix elements assigned with the parameters:
matrix _PHI_ = gg1-gg4;
Because symmetric matrices contain redundant elements, parameters are assigned only to the lower triangular elements (including the diagonal elements). As a result, the following elementwise specification reflects the preceding specification of matrix _PHI_:
matrix _PHI_ [1,1] = gg1,
[2,1] = gg2,
[2,2] = gg3,
[3,1] = gg4;
The case for lower triangular matrices is the same as the case for symmetric matrices. That is, only the lower triangular elements are valid elements for the parameter assignments.
For upper triangular matrices, only the upper triangular elements (including the diagonal elements) are valid for the parameter assignments. For example, consider the following specification of a 3  3 upper triangular matrix UPP:
3 upper triangular matrix UPP:
matrix UPP = gg1-gg4;
The matrix elements assigned with the parameters are the same as the following elementwise specification:
matrix UPP [1,1] = gg1,
[1,2] = gg2,
[1,3] = gg3,
[2,2] = gg4;
If a 4  4 diagonal matrix is specified by the preceding MATRIX statement, the parameters are assigned to the following elements: [1,1], [2,2], [3,3], and [4,4].
4 diagonal matrix is specified by the preceding MATRIX statement, the parameters are assigned to the following elements: [1,1], [2,2], [3,3], and [4,4].
Lastly, if there is no parameter-spec list for the unspecified location notation, all valid parameters in the matrix being specified are unnamed free parameters. For example, if  is a 4
is a 4  4 general rectangular matrix, the following specification assigns 16 unnamed free parameters to all of the elements in
4 general rectangular matrix, the following specification assigns 16 unnamed free parameters to all of the elements in  :
:
matrix A [,];
PROC CALIS generates parameters _Parm1, _Parm2, ..., _Parm16 to the elements [1,1], [1,2], [1,3], ..., [4,3], [4,4], respectively.
However, if 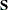 is a 4
is a 4  4 symmetric matrix, the following specification assigns only 10 unnamed free parameters to the lower triangular elements of
4 symmetric matrix, the following specification assigns only 10 unnamed free parameters to the lower triangular elements of 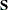 :
:
matrix S;
PROC CALIS generates parameters _Parm1, _Parm2, ..., _Parm10 to the elements [1,1], [2,1], [2,2], ..., [4,3], [4,4], respectively.
Row-and-Column Location: [i,j], [@i,j], [i,@j], or [@i,@j]
All these notations provide the starting row (i) and column (j numbers for the assignment of the parameters in the parameter-spec list. The notations are different in the way they proceed to the next element in the matrix. If no parameter-spec list is specified, only the single element [i,j] is an unnamed free parameter. For this [i,j] element, PROC CALIS generates a parameter name with the _Parm prefix followed by a unique integer (for example, _Parm1). If a parameter-spec list is specified, the assignment of parameters starts with the [i,j] element and proceeds to next element until all the parameters in the parameter-spec list are assigned. The following summarizes how the assignment of parameter proceeds, depending on the uses of the @ sign before the starting row or column number:
[i,j] specifies the [i,j] element, and proceeds to [i+1,j+1], [i+2,j+2], and so on.
[@i,j] specifies the [i,j] element, and proceeds to [i,j+1], [i,j+2], [i,j+3], and so on.
[i,@j] specifies the [i,j] element, and proceeds to [i+1,j], [i+2,j], [i+3,j], and so on.
[@i,@j] specifies the [i,j] element only.
Note:The syntax with the use of the @ sign is experimental in this version of PROC CALIS.
The following examples illustrates the usage of the row-and-column location notation.
The simplest case is the specification of a single element as an unnamed free parameter. For example, the following statement specifies that [1,4] in matrix  is an unnamed free parameter:
is an unnamed free parameter:
matrix A [1,4];
PROC CALIS generates a parameter name with the _Parm prefix for this element. In this case, using the @ sign before the row or column number is optional. That is, the following statements are all the same specification:
matrix A [1,4]; matrix A [@1,4]; matrix A [1,@4]; matrix A [@1,@4];
You can specify more than one unnamed free parameter by using multiple location specifications, as shown in the following example:
matrix A [1,4],[3,5];
Elements [1,4] and [3,5] of matrix  are both unnamed free parameters. However, when a parameter-spec list is specified after the location, more than one parameters might be specified. The use of the @ determines how the elements in the matrix are assigned with the parameters in the parameter-spec list. The following examples illustrate this under various situations.
are both unnamed free parameters. However, when a parameter-spec list is specified after the location, more than one parameters might be specified. The use of the @ determines how the elements in the matrix are assigned with the parameters in the parameter-spec list. The following examples illustrate this under various situations.
For example, consider the following specification of a 4  4 matrix general matrix
4 matrix general matrix  :
:
matrix A [1,1] = a b c;
The three parameters a, b, and c, are assigned to the matrix elements [1,1], [2,2], and [3,3], respectively. That is, this specification is equivalent to the following elementwise specification:
matrix A [1,1] = a , [2,2] = b , [3,3] = c ;
However, with the @ sign, the assignment is different. For example, consider the @ sign attached to the row number in the following specification:
matrix A [@1,1] = a b c;
The @ sign fixes the row number to 1. As a result, this specification is equivalent to the following elementwise specification:
matrix A [1,1] = a , [1,2] = b , [1,3] = c ;
Using the @ sign before the column number fixes the column number. For example, consider the following specification of matrix A:
matrix A [2,@2] = a b c;
The @ sign fixes the column number to 2. As a result, this specification is equivalent to the following elementwise specification:
matrix A [2,2] = a , [3,2] = b , [4,2] = c ;
If you put the @ sign in both of the row and column numbers, only one element is intended to be assigned. For example, the following specification means that only 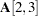 is assigned with the parameter a:
is assigned with the parameter a:
matrix A [@2,@3] = a;
But you could specify this simply as the statement without the @ sign:
matrix A [2,3] = a;
Notice that the matrix type does not play a role in determining the elements for the parameter assignments in the row-and-column location specification. You have to make sure that the parameters are assigned in the valid elements of the matrix. For example, suppose that 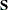 is a 4
is a 4  4 symmetric matrix and you specify the following statement for its elements:
4 symmetric matrix and you specify the following statement for its elements:
matrix A [@3,2] = a b c;
The elements to be assigned with the parameters a, b, and c, are [3,2], [3,3], and [3,4], respectively. However, because 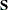 is symmetric, you can specify only the nonredundant elements in the lower triangular of
is symmetric, you can specify only the nonredundant elements in the lower triangular of 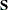 . Hence, the specification of the [3,4] element is not valid and it generates an error.
. Hence, the specification of the [3,4] element is not valid and it generates an error.
Row Location Only: [i,], [@i,], or [iset,]
All these notations provide the starting row [i1,] for the assignment of the parameters in parameter-spec, where i1 is i for the first two location notations or i1 is the first row specified in iset, where iset = (i1, i2, ...) is a set of row numbers. Because no column location is specified, the starting element is the first valid element in the i1-th row of the matrix.
If no parameter-spec list is specified, all the valid elements in the entire i1-th row of the matrix are unnamed free parameters. If a set of row numbers is specified in iset, all the valid elements in the all the rows specified in iset are unnamed free parameters.
If a parameter-spec list is specified, the assignment of parameters starts with the first valid elements of the i1-th row. The assignment proceeds to next valid elements in the same row. The [i,] specification proceeds row by row for parameter assignment while the [@i,] specification stays at the same i-th row. The [iset,] specification indicates and limits the sequence of rows to be assigned with the parameter in the parameter-spec list. The assignment stops when all the parameters in the parameter-spec list are assigned. The following summarizes how the assignment of parameters proceeds in more precise terms:
[i,] specifies the first valid element in row i and proceeds to the valid elements in rows i, i+1, i+2, ..., until all parameters in the parameter-spec list are assigned.
[@i,] specifies the first valid elements in row i and proceeds to the valid elements in the same row until all parameters in the parameter-spec list are assigned.
[iset,] specifies the first valid elements in row i1, where i1, i2, ...are the rows specified in iset. It proceeds to the valid elements in rows i1, i2, ..., until all parameters in the parameter-spec list are assigned.
The following examples illustrates the usage of the row locations.
The simplest case is the specification of all valid elements of a single row as unnamed free parameters. For example, the following specification of a 3  3 rectangular matrix
3 rectangular matrix  assigns unnamed free parameters to all the elements in the second row of matrix
assigns unnamed free parameters to all the elements in the second row of matrix  :
:
matrix A [2,];
PROC CALIS generates parameter names with the _Parm prefix for these elements. For example, the [2,1], [2,2], and [2,3] elements are named with _Parm1, _Parm2, and _Parm3, respectively.
Using the @ sign before the row number in this case is optional. That is, the following statement is the same specification:
matrix A [@2,];
If you specify a set of row numbers without the parameter-spec list, all valid elements of the specified rows are unnamed free parameters. For example, consider the following specification of a 6  6 symmetric matrix
6 symmetric matrix 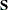 :
:
matrix S [1 3 5,];
This specification specifies unnamed free parameters for the lower triangular elements in the first, third, and fifth rows of matrix 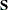 . It is equivalent to the following specification:
. It is equivalent to the following specification:
matrix S [1,],
[3,],
[5,];
As a result, this means that the following elements in matrix 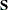 are free parameters: [1,1], [3,1], [3,2], [3,3], [5,1], [5,2], [5,3], [5,4], and [5,5]. Notice that only the elements in the lower triangular of those specified rows in
are free parameters: [1,1], [3,1], [3,2], [3,3], [5,1], [5,2], [5,3], [5,4], and [5,5]. Notice that only the elements in the lower triangular of those specified rows in 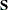 are free parameters. This shows that parameter assignment with the row location notation depends on the matrix type.
are free parameters. This shows that parameter assignment with the row location notation depends on the matrix type.
With the use of the parameter-spec list, the parameter assignment with the row location notation stops when all the parameters are assigned. For example, consider the following specification of a 4  4 general (rectangular) matrix
4 general (rectangular) matrix  :
:
matrix A [2,] = a b c;
The three parameters a, b, and c, are assigned to the matrix elements [2,1], [2,2], and [2,3], respectively. However, a different assignment of the parameters applies if you use the same specification for a 4  4 symmetric matrix
4 symmetric matrix 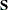 , as shown in the following statement:
, as shown in the following statement:
matrix S [2,] = a b c;
Because there are redundant elements in a symmetric matrix, you can specify only the lower triangular elements. Therefore, the row location specification is equivalent to the following elementwise specification:
matrix S [2,1] = a , [2,2] = b , [3,1] = c ;
When all the valid row elements are assigned with the parameters, the assignment proceeds to the next row. This is why the last parameter assignment is for  . The same assignment sequence applies to matrices with the lower triangular type (LOW).
. The same assignment sequence applies to matrices with the lower triangular type (LOW).
For matrices with the upper triangular matrix type (UPP), only the elements in the upper triangular are assigned. For example, consider a 4  4 upper triangular matrix
4 upper triangular matrix 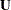 with the following row location specification:
with the following row location specification:
matrix U [2,] = a b c d;
The assignment of parameters is the same as the following elementwise specification:
matrix U [2,2] = a , [2,3] = b , [2,4] = c , [3,3] = d;
The first valid element in the second row of the 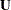 matrix is
matrix is  . Because all the valid elements in the second row are assigned with parameters, the last element has to go to the valid element in the next row. Hence, the parameter d is assigned to
. Because all the valid elements in the second row are assigned with parameters, the last element has to go to the valid element in the next row. Hence, the parameter d is assigned to 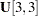 .
.
For matrices with the diagonal matrix type (DIA), only the diagonal elements are assigned. For example, consider a 4  4 upper diagonal matrix
4 upper diagonal matrix 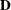 with the following row location specification:
with the following row location specification:
matrix D [2,] = a b c;
The assignment of parameters is the same as the following elementwise specification:
matrix D [2,2] = a , [3,3] = b , [4,4] = c ;
If you use an @ sign before the row number in the row location specification, the row number cannot move—it cannot proceed to the next row even if the valid elements in that row are already filled with the parameters in parameter-spec. All other behavior of the [@i,] specification is the same as that of the [i,] specification. For example, consider the following specification of a 4  4 general (rectangular) matrix
4 general (rectangular) matrix  :
:
matrix A [@2,] = a b c d;
The four parameters a, b, c, and d, are assigned to the matrix elements [2,1], [2,2], [2,3], and [2,4], respectively. This is exactly the same result as the following specification without the @ sign:
matrix A [2,] = a b c d;
Here, all the elements of the second row of matrix  are assigned with elements. However, if one more parameter is specified in the parameter-spec list, the behavior for the two types of row location specifications are different. The following specification without the @ sign proceeds to the next row for the last parameter:
are assigned with elements. However, if one more parameter is specified in the parameter-spec list, the behavior for the two types of row location specifications are different. The following specification without the @ sign proceeds to the next row for the last parameter:
matrix A [2,] = a b c d e;
That is, the parameter e is assigned to the 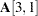 element. However, the following specification with the @ sign results in an out-of-bound error:
element. However, the following specification with the @ sign results in an out-of-bound error:
matrix A [@2,] = a b c d e;
The out-of-bound error is due to the fact that the row number must be fixed so that the parameter e is forced to be assigned to  , which does not exist.
, which does not exist.
However, the distinction between the row location specifications with and without the @ sign is not very important in common practice because in most cases you do not want the parameter assignment to proceed row after row automatically with a long list of parameters. For example, consider the following specification of a 4  4 symmetric matrix
4 symmetric matrix 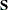 :
:
matrix S [2,] = s21 s22 s31 s32 s33 s41 s42 s43;
This specification is equivalent to the following specification:
matrix S [2,] = s21 s22, [3,] = s31 s32 s33, [4,] = s41 s42 s43;
Although this specification is not as concise as the preceding one, it specifies more clearly about how parameters are assigned to each of the three rows of the 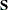 matrix. In this specification, you make sure that each of the three row location specifications has just enough parameters for the given row without proceeding to the next row for additional parameter assignments. With this kind of "careful" row location specifications, you do not need to use the @ sign before the row numbers at all.
matrix. In this specification, you make sure that each of the three row location specifications has just enough parameters for the given row without proceeding to the next row for additional parameter assignments. With this kind of "careful" row location specifications, you do not need to use the @ sign before the row numbers at all.
The last type of row location specification is the [iset,] notation, where iset means a set of row numbers. This specification type provides the set of row numbers for the assignment of the parameters in the parameter-spec list. For example, consider the following specification of a 4  4 general matrix
4 general matrix  :
:
matrix A [2 4,] = a21 a22 a23 a24 a41 a42 a43 a44;
This specification is equivalent to the following statement with two row location specifications:
matrix A [2,] = a21 a22 a23 a24, [4,] = a41 a42 a43 a44;
In other words, the assignment of parameters follows the order of rows provided in the iset. Notice that the iset notation merely provides the order of rows to be assigned with the parameters in the parameter-spec list; it is not an error if you provide a shorter parameter list than that of the total number of elements in the rows. For example, the following specification of a 4  4 general matrix
4 general matrix  is valid:
is valid:
matrix A [2 4,] = a21 a22 a23 a24;
This specification has the same results as the following statement with one row location:
matrix A [2,] = a21 a22 a23 a24;
However, a valid specification does not mean it is a good representation of the problem. Providing more rows in the iset specification than intended is simply not a good practice.
Although a shorter parameter-spec list is acceptable, a longer list results in an error. For example, the following specification of a 4  4 symmetric matrix
4 symmetric matrix 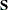 results in an error:
results in an error:
matrix S [2 to 3,] = s21 s22 s31 s32 s33 extra1 extra2;
The [2 to 3,] not only gives the sequence of the rows for the parameter assignment, it also limits the set of rows to assign. Because matrix 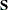 is symmetric and because only the second and the third rows are supposed to be assigned with the iset specification, the parameters extra1 and extra2 are excessive.
is symmetric and because only the second and the third rows are supposed to be assigned with the iset specification, the parameters extra1 and extra2 are excessive.
Column Location Only: [,j], [,@j], or [,jset]
These notations mirror that of the row location notations. Instead of the rows being specified, the columns are specified by these notations. Therefore, you can understand the column location notations the same way as the row location notations.
All these column location notations provide the starting column [,j1] for the assignment of the parameters in parameter-spec, where j1 is j for the first two location notations or j1 is the first column specified in jset, where jset = (j1, j2, ...) is a set of column numbers. Because no row location is specified, the starting element is the first valid element in the j1-th column of the matrix.
If no parameter-spec list is specified, all the valid elements in the entire j1-th column of the matrix are unnamed free parameters. If a set of column numbers is specified in jset, all the valid elements in the all the columns specified in jset are unnamed free parameters.
If a parameter-spec list is specified, the assignment of parameters starts with the first valid elements of the j1-th column. The assignment proceeds to next valid elements in the same column. The [,j] specification proceeds column by column for parameter assignment while the [,@j] specification stays at the same j-th column. The [,jset] specification indicates and limits the sequence of columns to be assigned with the parameter in the parameter-spec list. The assignment stops when all the parameters in the parameter-spec list are assigned. The following list summarizes how the assignment of parameters proceeds:
[,j] specifies the first valid element in column j and proceeds to the valid elements in columns j, j+1, j+2, ..., until all parameters in the parameter-spec list are assigned.
[,@j] specifies the first valid elements in column j and proceeds to the valid elements in the same column until all parameters in the parameter-spec list are assigned.
[,jset] specifies the first valid elements in column j1, where j1, j2, ...are the columns specified in jset. It proceeds to the valid elements in columns j1, j2, ..., until all parameters in the parameter-spec list are assigned.
See the section Row Location Only: [i,], [@i,], or [iset,] for examples, which are applicable to the usage of the column locations.
Row-and-Column-Sets Location: [iset,jset], [iset,j], or [i,jset]
These notations specify the sets of row and column elements for the assignment of the parameters in the parameter-spec list. In the first notation, you specify the set of row numbers in iset = (i1, i2, ...), and the set of column numbers in jset = (j1, j2, ...). The last two notations are special cases of the first notation. The [iset,j] notation specifies only one column with jset = j1 = j. The [i,jset] notation specifies only one row with iset = i1 = i. For the last two notations, adding the @ sign before j or i is optional. In general, the row-and-column-sets locations specify the matrix elements in the following order:
[i1,j1], [i1,j2], ...,
[i2,j1], [i2,j2], ...,
[i3,j1], [i3,j2], ...,
..., ..., ...,
[ir,j1], [ir,j2], ..., [ir,js]
where r represents the number of rows in the iset and s represents the number of columns in the jset. Note that this ordering of elements does not necessarily mean that all these elements are specified. The number of elements specified depends on the length of the parameter-spec list.
If no parameter-spec list is specified after the location notation, all the r  s elements specified in the iset and jset are unnamed free parameters. PROC CALIS generates parameter names with the _Parm prefix for these elements.
s elements specified in the iset and jset are unnamed free parameters. PROC CALIS generates parameter names with the _Parm prefix for these elements.
If a parameter-spec list is specified after the location notation, the total number of matrix elements that are assigned with the parameters is the same as the number of parameter specifications in the parameter-spec list.
The following examples illustrates the usage of the row-and-column-sets locations.
The simplest case is the specification of all elements in the iset and jset as free parameters, as shown in the following statement:
matrix _Gamma_ [2 3,4 1];
This means that _Gamma_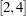 , _Gamma_
, _Gamma_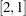 , _Gamma_
, _Gamma_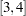 , and _Gamma_
, and _Gamma_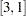 are all free parameters in the matrix. For these elements, PROC CALIS generates parameter names with the _Parm prefix followed by a unique integer (for example, _Parm1, _Parm2, ...). This row-and-column-sets location specification is the same as the following specification:
are all free parameters in the matrix. For these elements, PROC CALIS generates parameter names with the _Parm prefix followed by a unique integer (for example, _Parm1, _Parm2, ...). This row-and-column-sets location specification is the same as the following specification:
matrix _Gamma_ [2,4 1],[3,4 1];
It is also equivalent to the following elementwise specification:
matrix _Gamma_ [2,4],[2,1],[3,4],[3,1];
If you provide a parameter-spec list after the row-and-column-sets location, the parameters in the list are assigned to the matrix elements. For example, consider the following specification:
matrix _Gamma_ [2 3,4 1] = gamma1-gamma4;
This specification is equivalent to the following elementwise specification:
matrix _Gamma_ [2,4] = gamma1,
[2,1] = gamma2,
[3,4] = gamma3,
[3,1] = gamma4;
It is not necessary for all the elements specified in the row-and-column-sets location to be assigned with the parameters in the parameter-spec list. For example, the following iset and jset specify a maximum of six elements, but only five parameters are assigned as a result of a shorter parameter-spec list:
matrix _Gamma_ [2 to 4,1 5] = gamma1-gamma4;
This specification is equivalent to the following elementwise specification:
matrix _Gamma_ [2,1] = gamma1,
[2,5] = gamma2,
[3,1] = gamma3,
[3,5] = gamma4,
[4,1] = gamma5;
In this case, _Gamma_ is not specified and is fixed at zero by default.
is not specified and is fixed at zero by default.
With the row-and-column-sets location specifications, you need to be aware of the matrix type being specified. For example, the following specification of the symmetric matrix 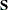 results in an out-of-bounds error:
results in an out-of-bounds error:
matrix S [1 2,1 2] = s1-s4;
This specification is equivalent to the following elementwise specification:
matrix S [1,1] = s1,
[1,2] = s2,
[2,1] = s3,
[2,2] = s4;
The specification of the 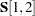 element is not valid because you can specify only the lower triangular elements of a symmetric matrix in PROC CALIS. The upper triangular elements are redundant and are taken into account by PROC CALIS during computations.
element is not valid because you can specify only the lower triangular elements of a symmetric matrix in PROC CALIS. The upper triangular elements are redundant and are taken into account by PROC CALIS during computations.
Specifying Fixed and Free Parameters in Model Matrices
For clarity in describing various location notations, the parameter-spec list contains only free parameters in the examples. In general, you can specify fixed values, free parameters, and initial values in the parameter-spec list. The syntax for the parameter-spec list is the same as the parameter-spec list for the VARIANCE statement. You can specify the following five types of the parameters in the MATRIX statement:
an unnamed free parameter
an initial value
a fixed value
a free parameter with a name provided
a free parameter with a name and initial value provided
The following example demonstrates these five types of specifications:
matrix A [1,2],
[1,3] = (.2),
[1,4] = .3,
[2,3] = a1,
[2,4] = a2(.5);
In this statement, 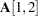 is an unnamed free parameter. For this element, PROC CALIS generates a parameter name with the _Parm prefix and appended with a unique integer (for example, _Parm1).
is an unnamed free parameter. For this element, PROC CALIS generates a parameter name with the _Parm prefix and appended with a unique integer (for example, _Parm1). 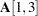 is an unnamed free parameter with an initial value of 0.2. PROC CALIS also generates a parameter name for this element.
is an unnamed free parameter with an initial value of 0.2. PROC CALIS also generates a parameter name for this element. 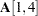 is fixed at 0.3. This value does not change in estimation.
is fixed at 0.3. This value does not change in estimation. 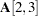 is a free parameter named a1. No initial value is given for this element.
is a free parameter named a1. No initial value is given for this element. 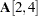 is a free parameter named a2 with an initial value of 0.5.
is a free parameter named a2 with an initial value of 0.5.
You can also specify different types of parameters in the parameter-spec list. The preceding specification is equivalent to the following specification:
matrix A [1,2],
[1 2,3 4] = (.2) .3 a1-a2 (.5);
Notice that 0.5 is the initial value for a2 but not for a1 because this specification is the same as:
matrix A [1,2],
[1 2,3 4] = (.2) .3 a1 a2(.5);
When you use parameter-spec lists with mixed parameters, you must be careful about how the initial value syntax is interpreted with and without a parameter name before it. With a parameter before the initial value, the initial value is for the parameter, as shown in the following statement:
matrix S [1,1] = s1 s2 (.2);
This specification is the same as the following elementwise specification:
matrix S [1,1] = s1,
[2,2] = s2(.2);
This means that 0.2 is the initial value of parameter s2, but not interpreted as an unnamed free parameter for  . If you do intend to set the free parameter s2 for
. If you do intend to set the free parameter s2 for 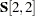 without an initial value and set the initial value 0.2 for
without an initial value and set the initial value 0.2 for  , you can use a null initial value for the s2 parameter, as shown in the following:
, you can use a null initial value for the s2 parameter, as shown in the following:
matrix S [1,1] = s1 s2() (.2);
This specification is the same as the following elementwise specification:
matrix S [1,1] = s1,
[2,2] = s2,
[3,3] = (.2);
Modifying a Parameter Specification from a Reference Model
If you define a new COSAN, LISMOD, or MSTRUCT model by using a reference (old) model in the REFMODEL statement, you might want to modify some parameter specifications from the MATRIX statement of the reference model before transferring the specifications to the new model. To change a particular matrix element specification from the reference model, you can simply respecify the same matrix element with the desired parameter specification in the MATRIX statement of the new model. To delete a particular matrix parameter from the reference model, you can specify the desired matrix element with a missing value specification in the MATRIX statement of the new model.
For example, suppose that _PHI_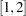 is a free parameter in the reference model but you do not want this matrix element be a free parameter in the new model, you can use the following specification in the new model:
is a free parameter in the reference model but you do not want this matrix element be a free parameter in the new model, you can use the following specification in the new model:
matrix _PHI_ [1,2] = .;
Notice that the missing value syntax is valid only when you use the REFMODEL statement. See the section Modifying a COSAN Model from a Reference Model for a more detailed example of COSAN model respecification. See the section Modifying a LISMOD Model from a Reference Model for a more detailed example of LISMOD model respecification. See the section Modifying an MSTRUCT Model from a Reference Model for a more detailed example of MSTRUCT model respecification.
Copyright © SAS Institute, Inc. All Rights Reserved.