PROC TCALIS: LINEQS Statement :: SAS/STAT(R) 9.2 User's Guide, Second Edition

The TCALIS Procedure

LINEQS Statement

LINEQS equation <, equation ...> ;

where equation represents:
dependent = term < + term ...>
and each term represents one of the following:
$\text{[math]}$ coefficient-name < (number) > variable-name
$\text{[math]}$ prefix-name < (number) > variable-name
$\text{[math]}$ < number > variable-name

The LINEQS statement is a main model specification statement that invokes the LINEQS modeling language. You can specify at most one LINEQS statement in a model, within the scope of either the PROC TCALIS statement or a MODEL statement. To completely specify a LINEQS model, you might need to add some subsidiary model specification statements. The following is the syntax for the LINEQS modeling language:

LINEQS model equations ;

STD partial variance parameters ;

COV covariance parameters ;

MEAN mean parameters ;

In the LINEQS statement, you use equations to specify the linear functional relations among manifest or latent variables. Equations in the LINEQS statement are separated by commas.

In the STD statement, you specify the variance parameters. In the COV statement, you specify the covariance parameters. In the MEAN statement, you specify the mean parameters. For details of these subsidiary model specification statements, see the syntax of these statements.

In the LINEQS statement, in addition to the functional relations among variables, you specify the coefficient parameters of interest in the equations. There are four types of parameters you can specify in equations, as shown in the following example:

   lineqs
      V1 = 1.      F1 + E1,
      V2 = b2      F1 + E2,
      V3 = b2      F1 + E3,
      V4 = b4 (.4) F1 + E4;

In this example, you have manifest variables V1–V4, which are related to a latent factor, denoted by F1, as specified in the equations. In each equation, you have one outcome variable (V-variable), one predictor variable (F1), and one error variable (E-variable). The following four types of parameters have been specified:

free or constrained parameters with starting values
The coefficient parameter b4 in the fourth equation is a free parameter to estimate. A starting value for a parameter can be specified inside parentheses following the parameter name. In this case, the starting value for b4 is 0.4. As shown in the equations, it is not constrained with any other coefficient parameters because b4 is specified at only one location.
free or constrained parameters without starting values
The coefficient parameter b2 in the second and the third equations is a parameter to estimate. No starting value is given for the parameter. With the same parameter name b2, the path coefficients with predictor variable F1 in the second and the third equation are thus implicitly constrained to be equal.
explicitly fixed parameter values
Any fixed constant preceding a predictor variable is a fixed parameter (for example, the constant coefficient 1 for F1 in the first equation).
implicitly fixed parameter values
If there is neither a parameter nor a constant preceding a predictor variable in an equation, the coefficient associated with that predictor variable is assumed to be a fixed parameter at one. For example, the coefficients preceding all error variables (E-variables) are fixed at 1. Any coefficients associated with unspecified predictor variables in equations are fixed zeros.

Parameters with no starting values will be initialized by various heuristic and effective methods in PROC TCALIS. See the section Initial Estimates for details.

If your model contains many unconstrained parameters and it is too cumbersome to find different parameter names, you can specify all those parameters by the same prefix name. A prefix name is a short name called "root" followed by double underscores '__'. Whenever a prefix name is encountered, the TCALIS procedure generates a parameter name by appending a unique integer to the root. Hence, the prefix name should have few characters so that the generated parameter name is not longer than thirty-two characters. To avoid unintentional equality constraints, the prefix names should not coincide with explicitly defined parameter names.

Certainly, coefficient parameters are only a subset of parameters of a model. Other parameters like variance, covariance and mean parameters should be specified in the subsidiary model statements for the LINEQS modeling language—that is, the COV, MEAN, and STD statements.

Representing Latent Variables in the LINEQS Model

Because latent variables are widely used in structural equation modeling, PROC TCALIS needs a way to identify different types of latent variables specified in the LINEQS model. This is accomplished by following some naming conventions for the latent variables. See the section Naming Variables in the LINEQS Model for details about these naming rules. Essentially, latent factors (systematic sources) must start with letter 'F' or 'f'. Error terms must start with letter 'E', 'e', 'D', or 'd'. Prefix 'E' or 'e' represents the error term of an endogenous manifest variable. Prefix 'D' or 'd' represent represents disturbance (or error) term of an endogenous latent variable. Although 'D' and 'E' variables are conceptually different, for modeling purposes 'D' and 'E' prefixes are not distinguished in PROC TCALIS. Essentially, only the distinction between latent factors (systematic sources) and errors or disturbances (unsystematic sources) is critical in specifying a proper model analyzed by PROC TCALIS. Manifest variables in PROC TCALIS do not need to follow additional naming rules beyond those required by the general SAS system—they only need to have references in the input data set.

Types of Variables and Semantic Rules of Equations

Depending on their roles in the system of equations, variables in a LINEQS model can be classified into endogenous or exogenous. An endogenous variable is a variable that serves as an outcome variable (left-hand side of an equation) in one of the equations. All other variables are exogenous variables, including those manifest variables that never appear in any places of any equation but are specified in the VAR statement.

The syntactic rules for equations are far from sufficient to define the system of equations that the LINEQS model would accept. You must also observe the following semantic rules:

Only manifest or latent variables can be endogenous. This means that you cannot specify any error or disturbances variables on the left-hand side of equations. This also means that error and disturbance variables are always exogenous in the LINEQS model.
An endogenous variable appearing on the left-hand side of an equation cannot appear on the left-hand side of another equation. In other words, you have to specify all the predictors for an endogenous variable in a single equation.
An endogenous variable appearing on the left-hand side of an equation cannot appear on the right-hand side of the same equation.
Each equation must contain one and only one unique error term, be it an E-variable for manifest outcome variable or a D-variable for latent outcome variable. If, indeed, you want to specify an equation without an error term, you might equivalently set the variance of the error term to a fixed zero in the STD statement.

Mean Structures in Equations

To fit a LINEQS model with mean structures, you can specify the MEANSTR option in the PROC TCALIS or the associated MODEL statement. Alternatively, you can use the Intercept variable in equations for including intercept terms or the MEAN statement to specify the mean parameters. Conceptually, the Intercept variable is a special "variable" containing the value one for each observation. You do not need to have this variable in your input data set, nor do you need to generate it in the DATA step. It serves as a notational convenience in the LINEQS modeling language. The actual intercept parameter is expressed as a coefficient parameter with the intercept variable. For example, consider the following LINEQS model specification.

   lineqs
      V1 = a1 (10) Intercept +         F1 + E1,
      V2 =                   + b2      F1 + E2,
      V3 = a2      Intercept + b2      F1 + E3,
      V4 = a2      Intercept + b4 (.4) F1 + E4;

In the first equation, a1, with a starting value at 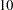$\text{[math]}$ , is the intercept parameter for v1. The intercept parameters for V3 and V4 are constrained to be the same. They are named a2 in the equations. Even though there is no Intercept variable specified in the equation for endogenous variable V2, its intercept parameter is assumed to be a fixed zero. This is because once you use at least one Intercept variable in an equation or you specify at least one mean parameter in the MEAN statement, mean structure analysis is activated and all mean and intercept parameters have default values at zero, unless you specify parameter names or other fixed values explicitly in the equations or in the MEAN statement.

Modifying a LINEQS Model from a Reference Model

In this section, it is assumed that you use a REFMODEL statement within the scope of a MODEL statement and the reference model (or base model) is a LINEQS model. The reference model will be referred to as the old model, while the model being defined is referred to as the new model. If the new model is not intended to be an exact copy of the old model, you can use the following extended LINEQS modeling language to make modifications within the scope of the MODEL statement for the new model.

The syntax of the extended LINEQS modeling language is the same as that of the ordinary LINEQS modeling language (see the section LINEQS Statement):

LINEQS model equations ;

STD partial variance parameters ;

COV covariance parameters ;

MEAN mean parameters ;

The new model is formed by integrating with the old model in the following ways:

Duplication:: If you do not specify in the new model an equation with an outcome variable (that is, a variable on the left of the equal sign) that exists in the old model, the equation with that outcome variable in the old model is duplicated in the new model. For specifications other than the LINEQS statement, if you do not specify in the new model a parameter location that exists in the old model, the old parameter specification is duplicated in the new model.
Addition:: If you specify in the new model an equation with an outcome variable that does not exist as an outcome variable in the equations of the old model, the equation is added in the new model. For specifications other than the LINEQS statement, if you specify in the new model a parameter location that does not exist in the old model, the new parameter specification is added in the new model.
Deletion:: If you specify in the new model an equation with an outcome variable that also exists as an outcome variable in an equation of the old model and you specify the missing value '.' as the only term on the right-hand side of the equation in the new model, the equation with the same outcome variable in the old model is not copied into the new model. For specifications other than the LINEQS statement, if you specify in the new model a parameter location that also exists in the old model and the new parameter is denoted by the missing value '.', the old parameter specification is not copied into the new model.
Replacement:: If you specify in the new model an equation with an outcome variable that also exists as an outcome variable in an equation of the model and the right-hand side of the equation in the new model is not denoted by the missing value '.', the new equation replaces the old equation with the same outcome variable in the new model. For specifications other than the LINEQS statement, if you specify in the new model a parameter location that also exists in the old model and the new parameter is not denoted by the missing value '.', the new parameter specification replaces the old one in the new model.

For example, in the following two-group analysis you specify model 2 by referring to model 1 in the REFMODEL statement.

   proc tcalis;
      group 1 / data=d1;
      group 2 / data=d2;
      model 1 / group=1;
         lineqs
            V1   =      1 F1   + E1,
            V2   =  load1 F1   + E2,
            V3   =  load2 F1   + E3,
            F1   =     b1 V4   + b2 V5 + b3 V6 + D1;
         std 
            E1-E3  = ve1-ve3,
            D1     = vd1,
            V4-V6  = phi4-phi6;
         cov
            E1 E2 = cve12;
      model 2 / group=2;
         refmodel 1;
         lineqs
            V3   = load1 F1 + E3;
         cov
            E1 E2 = ., 
            E2 E3 = cve23;
      run;

Model 2 is the new model which refers to the old model, model 1. This example illustrates the four types of model integration:

Duplication: All equations, except the one with outcome variable V3, in the old model are duplicated in the new model. All specifications in the STD and COV statements, except the covariance between E1 and E2, in the old model are also duplicated in the new model.
Addition: The parameter cve23 for the covariance between E2 and E3 is added in the new model.
Deletion: The specification of covariance between E1 and E2 in the old model is not copied into the new model, as indicated by the missing value '.' specified in the new model.
Replacement: The equation with V3 as the outcome variable in the old model is replaced with a new equation in the model. The new equation uses parameter load1 so that it is now constrained to be the same as the regression coefficient in the equation with V2 as the outcome variable.

Note: This procedure is experimental.

Top of Page