Single Failure Time Variable

Let 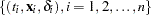be the observed data. Let 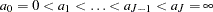be a partition of the time axis.

Hazards in Original Scale

The hazard function for subject is

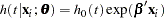where

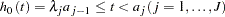The baseline cumulative hazard function is

where

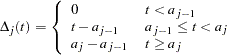The log likelihood is given by

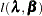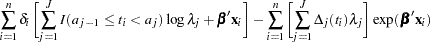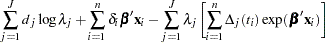where .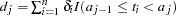

Note that for 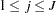, the full conditional for 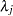is log-concave only when 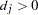, but the full conditionals for the 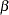’s are always log-concave.

For a given 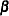, 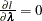gives

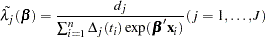Substituting these values into 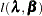gives the profile log likelihood for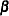

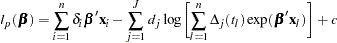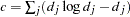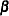where . Since the constant does not depend on , it can be discarded from in the optimization.

The MLE 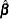of 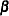is obtained by maximizing

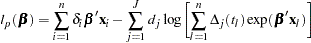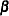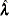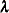with respect to , and the MLE of is given by

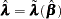Let

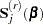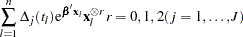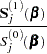The partial derivatives of are

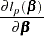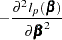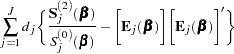The asymptotic covariance matrix for 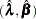is obtained as the inverse of the information matrix given by

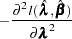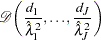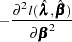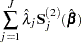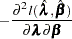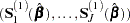See Example 6.5.1 in Lawless (2003) for details.

Hazards in Log Scale

By letting

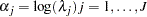you can build a prior correlation among the 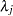’s by using a correlated prior 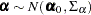, where .

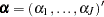The log likelihood is given by

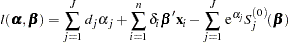Then the MLE of 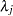is given by

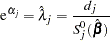Note that the full conditionals for ’s and 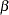’s are always log-concave.

The asymptotic covariance matrix for 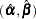is obtained as the inverse of the information matrix formed by

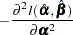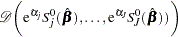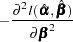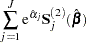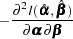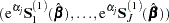Counting Process Style of Input

Let 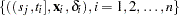be the observed data. Let 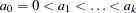be a partition of the time axis, where 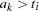for all .

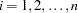Replacing 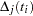with

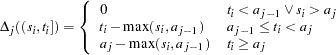the formulation for the single failure time variable applies.