| The PHREG Procedure |
Priors for Model Parameters
For a Cox model, the model parameters are the regression coefficients. For a piecewise exponential model, the model parameters consist of the regression coefficients and the hazards or log-hazards. The priors for the hazards and the priors for the regression coefficients are assumed to be independent, while you can have a joint multivariate normal prior for the log-hazards and the regression coefficients.
Hazard Parameters
Let 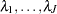 be the constant baseline hazards.
be the constant baseline hazards.
Improper Prior
The joint prior density is given by
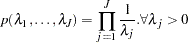 |
This prior is improper (nonintegrable), but the posterior distribution is proper as long as there is at least one event time in each of the constant hazard intervals.
Uniform Prior
The joint prior density is given by
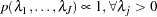 |
This prior is improper (nonintegrable), but the posteriors are proper as long as there is at least one event time in each of the constant hazard intervals.
Gamma Prior
The gamma distribution 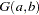 has a pdf
has a pdf
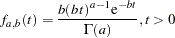 |
where  is the shape parameter and
is the shape parameter and 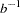 is the scale parameter. The mean is
is the scale parameter. The mean is 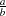 and the variance is
and the variance is 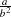 .
.
Independent Gamma Prior
Suppose for 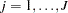 ,
, 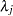 has an independent
has an independent 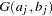 prior. The joint prior density is given by
prior. The joint prior density is given by
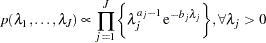 |
AR1 Prior
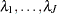 are correlated as follows:
are correlated as follows:
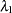 |
 |
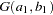 |
|||
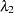 |
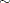 |
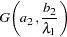 |
|||
 |
 |
 |
|||
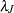 |
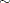 |
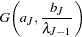 |
The joint prior density is given by
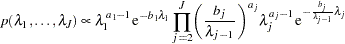 |
Log-Hazard Parameters
Write 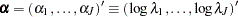 .
.
Uniform Prior
The joint prior density is given by
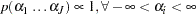 |
Note that the uniform prior for the log-hazards is the same as the improper prior for the hazards.
Normal Prior
Assume  has a multivariate normal prior with mean vector
has a multivariate normal prior with mean vector 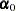 and covariance matrix
and covariance matrix 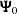 . The joint prior density is given by
. The joint prior density is given by
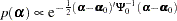 |
Regression Coefficients
Let  be the vector of regression coefficients.
be the vector of regression coefficients.
Uniform Prior
The joint prior density is given by
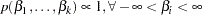 |
This prior is improper, but the posterior distributions for 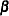 are proper.
are proper.
Normal Prior
Assume 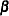 has a multivariate normal prior with mean vector
has a multivariate normal prior with mean vector 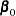 and covariance matrix
and covariance matrix 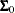 . The joint prior density is given by
. The joint prior density is given by
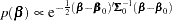 |
Joint Multivariate Normal Prior for Log-Hazards and Regression Coefficients
Assume 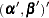 has a multivariate normal prior with mean vector
has a multivariate normal prior with mean vector 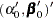 and covariance matrix
and covariance matrix 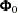 . The joint prior density is given by
. The joint prior density is given by
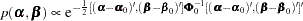 |
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.