PROC MIXED: Known G and R :: SAS/STAT(R) 9.2 User's Guide, Second Edition

The MIXED Procedure

Example 56.4 Known G and R

This animal breeding example from Henderson (1984, p. 48) considers multiple traits. The data are artificial and consist of measurements of two traits on three animals, but the second trait of the third animal is missing. Assuming an additive genetic model, you can use PROC MIXED to predict the breeding value of both traits on all three animals and also to predict the second trait of the third animal. The data are as follows:

   data h;
     input Trait Animal Y;
     datalines;
   1 1 6
   1 2 8
   1 3 7
   2 1 9
   2 2 5
   2 3 .
   ;

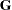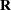Both $\text{[math]}$ and $\text{[math]}$ are known.

$\text{[math]}$

In order to read 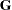$\text{[math]}$ into PROC MIXED by using the GDATA= option in the RANDOM statement, perform the following DATA step:

   data g;
      input Row Col1-Col6;
      datalines;
   1  2  1  1  2   1     1
   2  1  2 .5  1   2    .5
   3  1 .5  2  1    .5  2
   4  2  1  1  3   1.5  1.5
   5  1  2 .5  1.5 3     .75
   6  1 .5  2  1.5  .75 3
   ;

The preceding data are in the dense representation for a GDATA= data set. You can also construct a data set with the sparse representation by using Row, Col, and Value variables, although this would require 21 observations instead of 6 for this example.

The PROC MIXED statements are as follows:

   proc mixed data=h mmeq mmeqsol;
      class Trait Animal;
      model Y = Trait / noint s outp=predicted;
      random Trait*Animal / type=un gdata=g g gi s;
      repeated / type=un sub=Animal r ri;
      parms (4) (1) (5) / noiter;
   run;
   proc print data=predicted;
   run;

The MMEQ and MMEQSOL options request the mixed model equations and their solution. The variables Trait and Animal are classification variables, and Trait defines the entire 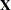$\text{[math]}$ matrix for the fixed-effects portion of the model, since the intercept is omitted with the NOINT option. The fixed-effects solution vector and predicted values are also requested by using the S and OUTP= options, respectively.

The random effect Trait*Animal leads to a 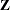$\text{[math]}$ matrix with six columns, the first five corresponding to the identity matrix and the last consisting of 0s. An unstructured 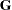$\text{[math]}$ matrix is specified by using the TYPE=UN option, and it is read into PROC MIXED from a SAS data set by using the GDATA=G specification. 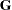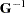The G and GI options request the display of $\text{[math]}$ and $\text{[math]}$ , respectively. The S option requests that the random-effects solution vector be displayed.

Note that the preceding 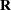$\text{[math]}$ matrix is block diagonal if the data are sorted by animals. The REPEATED statement exploits this fact by requesting 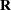$\text{[math]}$ to have unstructured 2 $\text{[math]}$ 2 blocks corresponding to animals, which are the subjects. The R and RI options request that the estimated 2 $\text{[math]}$ 2 blocks for the first animal and its inverse be displayed. The PARMS statement lists the parameters of this 2 $\text{[math]}$ 2 matrix. 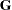Note that the parameters from $\text{[math]}$ are not specified in the PARMS statement because they have already been assigned by using the GDATA= option in the RANDOM statement. The NOITER option prevents PROC MIXED from computing residual (restricted) maximum likelihood estimates; instead, the known values are used for inferences.

The results from this analysis are shown in Output 56.4.1–Output 56.4.12.

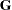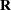The "Unstructured" covariance structure (Output 56.4.1) applies to both $\text{[math]}$ and $\text{[math]}$ here. The levels of Trait and Animal have been specified correctly.

Output 56.4.1 Model and Class Level Information

The Mixed Procedure

Model Information
Data Set	WORK.H
Dependent Variable	Y
Covariance Structure	Unstructured
Subject Effect	Animal
Estimation Method	REML
Residual Variance Method	None
Fixed Effects SE Method	Model-Based
Degrees of Freedom Method	Containment

Class Level Information
Class	Levels	Values
Trait	2	1 2
Animal	3	1 2 3

The three covariance parameters indicated in Output 56.4.2 correspond to those from the 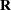$\text{[math]}$ matrix. Those from 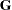$\text{[math]}$ are considered fixed and known because of the GDATA= option.

Output 56.4.2 Model Dimensions and Number of Observations

Dimensions
Covariance Parameters	3
Columns in X	2
Columns in Z	6
Subjects	1
Max Obs Per Subject	6

Number of Observations
Number of Observations Read	6
Number of Observations Used	5
Number of Observations Not Used	1

Because starting values for the covariance parameters are specified in the PARMS statement, the MIXED procedure prints the residual (restricted) log likelihood at the starting values. Because of the NOITER option in the PARMS statement, this is also the final log likelihood in this analysis (Output 56.4.3).

Output 56.4.3 REML Log Likelihood

Parameter Search
CovP1	CovP2	CovP3	Res Log Like	-2 Res Log Like
4.0000	1.0000	5.0000	-7.3731	14.7463

The block of 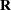$\text{[math]}$ corresponding to the first animal and the inverse of this block are shown in Output 56.4.4.

Output 56.4.4 Inverse R Matrix

Estimated R Matrix for Animal 1
Row	Col1	Col2
1	4.0000	1.0000
2	1.0000	5.0000

Estimated Inv(R) Matrix for Animal 1
Row	Col1	Col2
1	0.2632	-0.05263
2	-0.05263	0.2105

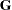The $\text{[math]}$ matrix as specified in the GDATA= data set and its inverse are shown in Output 56.4.5 and Output 56.4.6.

Output 56.4.5 G Matrix

Estimated G Matrix
Row	Effect	Trait	Animal	Col1	Col2	Col3	Col4	Col5	Col6
1	Trait*Animal	1	1	2.0000	1.0000	1.0000	2.0000	1.0000	1.0000
2	Trait*Animal	1	2	1.0000	2.0000	0.5000	1.0000	2.0000	0.5000
3	Trait*Animal	1	3	1.0000	0.5000	2.0000	1.0000	0.5000	2.0000
4	Trait*Animal	2	1	2.0000	1.0000	1.0000	3.0000	1.5000	1.5000
5	Trait*Animal	2	2	1.0000	2.0000	0.5000	1.5000	3.0000	0.7500
6	Trait*Animal	2	3	1.0000	0.5000	2.0000	1.5000	0.7500	3.0000

Output 56.4.6 Inverse G Matrix

Estimated Inv(G) Matrix
Row	Effect	Trait	Animal	Col1	Col2	Col3	Col4	Col5	Col6
1	Trait*Animal	1	1	2.5000	-1.0000	-1.0000	-1.6667	0.6667	0.6667
2	Trait*Animal	1	2	-1.0000	2.0000		0.6667	-1.3333
3	Trait*Animal	1	3	-1.0000		2.0000	0.6667		-1.3333
4	Trait*Animal	2	1	-1.6667	0.6667	0.6667	1.6667	-0.6667	-0.6667
5	Trait*Animal	2	2	0.6667	-1.3333		-0.6667	1.3333
6	Trait*Animal	2	3	0.6667		-1.3333	-0.6667		1.3333

The table of covariance parameter estimates in Output 56.4.7 displays only the parameters in 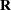$\text{[math]}$ . Because of the GDATA= option in the RANDOM statement, the G-side parameters do not participate in the parameter estimation process. Because of the NOITER option in the PARMS statement, however, the R-side parameters in this output are identical to their starting values.

Output 56.4.7 R-Side Covariance Parameters

Covariance Parameter Estimates
Cov Parm	Subject	Estimate
UN(1,1)	Animal	4.0000
UN(2,1)	Animal	1.0000
UN(2,2)	Animal	5.0000

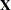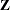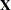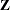The coefficients of the mixed model equations in Output 56.4.8 agree with Henderson (1984, p. 55). Recall from Output 56.4.1 that there are 2 columns in $\text{[math]}$ and 6 columns in $\text{[math]}$ . The first 8 columns of the mixed model equations correspond to the $\text{[math]}$ and $\text{[math]}$ components. Column 9 represents the Y border.

Output 56.4.8 Mixed Model Equations with Y Border

Mixed Model Equations
Row	Effect	Trait	Animal	Col1	Col2	Col3	Col4	Col5	Col6	Col7	Col8	Col9
1	Trait	1		0.7763	-0.1053	0.2632	0.2632	0.2500	-0.05263	-0.05263		4.6974
2	Trait	2		-0.1053	0.4211	-0.05263	-0.05263		0.2105	0.2105		2.2105
3	Trait*Animal	1	1	0.2632	-0.05263	2.7632	-1.0000	-1.0000	-1.7193	0.6667	0.6667	1.1053
4	Trait*Animal	1	2	0.2632	-0.05263	-1.0000	2.2632		0.6667	-1.3860		1.8421
5	Trait*Animal	1	3	0.2500		-1.0000		2.2500	0.6667		-1.3333	1.7500
6	Trait*Animal	2	1	-0.05263	0.2105	-1.7193	0.6667	0.6667	1.8772	-0.6667	-0.6667	1.5789
7	Trait*Animal	2	2	-0.05263	0.2105	0.6667	-1.3860		-0.6667	1.5439		0.6316
8	Trait*Animal	2	3			0.6667		-1.3333	-0.6667		1.3333

The solution to the mixed model equations also matches that given by Henderson (1984, p. 55). After solving the augmented mixed model equations, you can find the solutions for fixed and random effects in the last column (Output 56.4.9).

Output 56.4.9 Solutions of the Mixed Model Equations with Y Border

Mixed Model Equations Solution
Row	Effect	Trait	Animal	Col1	Col2	Col3	Col4	Col5	Col6	Col7	Col8	Col9
1	Trait	1		2.5508	1.5685	-1.3047	-1.1775	-1.1701	-1.3002	-1.1821	-1.1678	6.9909
2	Trait	2		1.5685	4.5539	-1.4112	-1.3534	-0.9410	-2.1592	-2.1055	-1.3149	6.9959
3	Trait*Animal	1	1	-1.3047	-1.4112	1.8282	1.0652	1.0206	1.8010	1.0925	1.0070	0.05450
4	Trait*Animal	1	2	-1.1775	-1.3534	1.0652	1.7589	0.7085	1.0900	1.7341	0.7209	-0.04955
5	Trait*Animal	1	3	-1.1701	-0.9410	1.0206	0.7085	1.7812	1.0095	0.7197	1.7756	0.02230
6	Trait*Animal	2	1	-1.3002	-2.1592	1.8010	1.0900	1.0095	2.7518	1.6392	1.4849	0.2651
7	Trait*Animal	2	2	-1.1821	-2.1055	1.0925	1.7341	0.7197	1.6392	2.6874	0.9930	-0.2601
8	Trait*Animal	2	3	-1.1678	-1.3149	1.0070	0.7209	1.7756	1.4849	0.9930	2.7645	0.1276

The solutions for the fixed and random effects in Output 56.4.10 correspond to the last column in Output 56.4.9. Note that the standard errors for the fixed effects and the prediction standard errors for the random effects are the square root values of the diagonal entries in the solution of the mixed model equations (Output 56.4.9).

Output 56.4.10 Solutions for Fixed and Random Effects

Solution for Fixed Effects
Effect	Trait	Estimate	Standard Error	DF	t Value	Pr > \|t\|
Trait	1	6.9909	1.5971	3	4.38	0.0221
Trait	2	6.9959	2.1340	3	3.28	0.0465

Solution for Random Effects
Effect	Trait	Animal	Estimate	Std Err Pred	DF	t Value	Pr > \|t\|
Trait*Animal	1	1	0.05450	1.3521	0	0.04	.
Trait*Animal	1	2	-0.04955	1.3262	0	-0.04	.
Trait*Animal	1	3	0.02230	1.3346	0	0.02	.
Trait*Animal	2	1	0.2651	1.6589	0	0.16	.
Trait*Animal	2	2	-0.2601	1.6393	0	-0.16	.
Trait*Animal	2	3	0.1276	1.6627	0	0.08	.

The estimates for the two traits are nearly identical, but the standard error of the second trait is larger because of the missing observation.

The Estimate column in the "Solution for Random Effects" table lists the best linear unbiased predictions (BLUPs) of the breeding values of both traits for all three animals. The p-values are missing because the default containment method for computing degrees of freedom results in zero degrees of freedom for the random effects parameter tests.

Output 56.4.11 Significance Test Comparing Traits

Type 3 Tests of Fixed Effects
Effect	Num DF	Den DF	F Value	Pr > F
Trait	2	3	10.59	0.0437

The two estimated traits are significantly different from zero at the 5% level (Output 56.4.11).

Output 56.4.12 displays the predicted values of the observations based on the trait and breeding value estimates—that is, the fixed and random effects.

Output 56.4.12 Predicted Observations

Obs	Trait	Animal	Y	Pred	StdErrPred	Alpha	Lower	Upper	Resid
1	1	1	6	7.04542	1.33027	0.05	.	.	-1.04542
2	1	2	8	6.94137	1.39806	0.05	.	.	1.05863
3	1	3	7	7.01321	1.41129	0.05	.	.	-0.01321
4	2	1	9	7.26094	1.72839	0.05	.	.	1.73906
5	2	2	5	6.73576	1.74077	0.05	.	.	-1.73576
6	2	3	.	7.12015	2.99088	0.05	.	.	.

The predicted values are not the predictions of future records in the sense that they do not contain a component corresponding to a new observational error. See Henderson (1984) for information about predicting future records. The Lower and Upper columns usually contain confidence limits for the predicted values; they are missing here because the random-effects parameter degrees of freedom equals 0.

Top of Page