PROC MIXED: PARMS Statement :: SAS/STAT(R) 9.2 User's Guide, Second Edition

The MIXED Procedure

PARMS Statement

PARMS (value-list) ...</ options> ;

The PARMS statement specifies initial values for the covariance parameters, or it requests a grid search over several values of these parameters. You must specify the values in the order in which they appear in the "Covariance Parameter Estimates" table.

The value-list specification can take any of several forms:

m: a single value
$\text{[math]}$: several values
m to n: a sequence where m equals the starting value, n equals the ending value, and the increment equals 1
m to n by i: a sequence where m equals the starting value, n equals the ending value, and the increment equals i
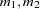$\text{[math]}$ to $\text{[math]}$: mixed values and sequences

You can use the PARMS statement to input known parameters. Referring to the split-plot example (Example 56.1), suppose the three variance components are known to be 60, 20, and 6. The SAS statements to fix the variance components at these values are as follows:

   proc mixed data=sp noprofile;
      class Block A B;
      model Y = A B A*B;
      random Block A*Block;
      parms (60) (20) (6) / noiter;
   run;

The NOPROFILE option requests PROC MIXED to refrain from profiling the residual variance parameter during its calculations, thereby enabling its value to be held at 6 as specified in the PARMS statement. The NOITER option prevents any Newton-Raphson iterations so that the subsequent results are based on the given variance components. You can also specify known parameters of 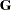$\text{[math]}$ by using the GDATA= option in the RANDOM statement.

If you specify more than one set of initial values, PROC MIXED performs a grid search of the likelihood surface and uses the best point on the grid for subsequent analysis. Specifying a large number of grid points can result in long computing times. The grid search feature is also useful for exploring the likelihood surface. (See Example 56.3.)

The results from the PARMS statement are the values of the parameters on the specified grid (denoted by CovP1–CovPn), the residual variance (possibly estimated) for models with a residual variance parameter, and various functions of the likelihood.

For ODS purposes, the name of the "Parameter Search" table is "ParmSearch."

You can specify the following options in the PARMS statement after a slash (/).

HOLD=value-list

EQCONS=value-list

specifies which parameter values PROC MIXED should hold to equal the specified values. For example, the following statement constrains the first and third covariance parameters to equal 5 and 2, respectively:

   parms (5) (3) (2) (3) / hold=1,3;

LOGDETH

evaluates the log determinant of the Hessian matrix for each point specified in the PARMS statement. A Log Det H column is added to the "Parameter Search" table.

LOWERB=value-list

enables you to specify lower boundary constraints on the covariance parameters. The value-list specification is a list of numbers or missing values (.) separated by commas. You must list the numbers in the order that PROC MIXED uses for the covariance parameters, and each number corresponds to the lower boundary constraint. A missing value instructs PROC MIXED to use its default constraint, and if you do not specify numbers for all of the covariance parameters, PROC MIXED assumes the remaining ones are missing.

An example for which this option is useful is when you want to constrain the 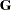$\text{[math]}$ matrix to be positive definite in order to avoid the more computationally intensive algorithms required when 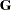$\text{[math]}$ becomes singular. The corresponding statements for a random coefficients model are as follows:

   proc mixed;
      class person;
      model y = time;
      random int time / type=fa0(2) sub=person;
      parms / lowerb=1e-4,.,1e-4;
   run;

Here the TYPE=FA0(2) structure is used in order to specify a Cholesky root parameterization for the $\text{[math]}$ unstructured blocks in 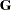$\text{[math]}$ . This parameterization ensures that the 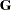$\text{[math]}$ matrix is nonnegative definite, and the PARMS statement then ensures that it is positive definite by constraining the two diagonal terms to be greater than or equal to 1E $\text{[math]}$ 4.

NOBOUND

requests the removal of boundary constraints on covariance parameters. For example, variance components have a default lower boundary constraint of 0, and the NOBOUND option allows their estimates to be negative.

NOITER

requests that no Newton-Raphson iterations be performed and that PROC MIXED use the best value from the grid search to perform inferences. By default, iterations begin at the best value from the PARMS grid search.

NOPROFILE

specifies a different computational method for the residual variance during the grid search. By default, PROC MIXED estimates this parameter by using the profile likelihood when appropriate. This estimate is displayed in the Variance column of the "Parameter Search" table. The NOPROFILE option suppresses the profiling and uses the actual value of the specified variance in the likelihood calculations.

OLS

requests starting values corresponding to the usual general linear model. Specifically, all variances and covariances are set to zero except for the residual variance, which is set equal to its ordinary least squares (OLS) estimate. This option is useful when the default MIVQUE0 procedure produces poor starting values for the optimization process.

PARMSDATA=SAS-data-set

PDATA=SAS-data-set

reads in covariance parameter values from a SAS data set. The data set should contain the Est or Covp1–Covpn variables.

RATIOS

indicates that ratios with the residual variance are specified instead of the covariance parameters themselves. The default is to use the individual covariance parameters.

UPPERB=value-list

enables you to specify upper boundary constraints on the covariance parameters. The value-list specification is a list of numbers or missing values (.) separated by commas. You must list the numbers in the order that PROC MIXED uses for the covariance parameters, and each number corresponds to the upper boundary constraint. A missing value instructs PROC MIXED to use its default constraint, and if you do not specify numbers for all of the covariance parameters, PROC MIXED assumes that the remaining ones are missing.

Top of Page