| The MCMC Procedure |
| Standard Distributions |
Table 52.3 through Table 52.30 show all densities that PROC MCMC recognizes. These densities can be used in the MODEL, PRIOR, and HYPERPRIOR statements. See the section Using Density Functions in the Programming Statements for information about how to use distributions in the programming statements. To specify an arbitrary distribution, you can use the functions GENERAL and DGENERAL. See the section Specifying a New Distribution for more details. See the section Truncation and Censoring for tips on how to work with truncated distributions and censoring data.
PROC specification |
beta( |
density |
|
parameter restriction |
|
range |
|
mean |
|
variance |
|
mode |
|
random number |
if |
PROC specification |
binary( |
density |
|
parameter restriction |
|
range |
|
mean |
round |
variance |
|
mode |
|
random number |
generate |
PROC specification |
binomial( |
density |
|
parameter restriction |
|
range |
|
mean |
|
variance |
|
mode |
|
PROC specification |
cauchy( |
density |
|
parameter restriction |
|
range |
|
mean |
does not exist |
variance |
does not exist |
mode |
|
random number |
generate |
PROC specification |
chisq( |
density |
|
parameter restriction |
|
range |
|
mean |
|
variance |
|
mode |
|
random number |
|
PROC specification |
expchisq( |
density |
|
parameter restriction |
|
range |
|
mode |
|
random number |
generate |
relationship to the |
|
PROC specification |
expexpon(scale = |
expexpon(iscale = |
density |
|
|
parameter restriction |
|
|
range |
|
same |
mode |
|
|
random number |
generate |
|
relationship to the Expon distribution |
|
|
PROC specification |
expgamma( |
expgamma( |
density |
|
|
parameter restriction |
|
|
range |
|
same |
mode |
|
|
random number |
generate |
|
relationship to the |
|
|
PROC specification |
expichisq( |
density |
|
parameter restriction |
|
range |
|
mode |
|
random number |
generate |
relationship to the |
|
PROC specification |
expigamma( |
expigamma( |
density |
|
|
parameter restriction |
|
|
range |
|
same |
mode |
|
|
random number |
generate |
|
relationship to the |
|
|
PROC specification |
expsichisq( |
density |
|
parameter restriction |
|
range |
|
mode |
|
random number |
generate |
relationship to the |
|
PROC specification |
expon(scale = |
expon(iscale = |
density |
|
|
parameter restriction |
|
|
range |
|
same |
mean |
|
|
variance |
|
|
mode |
|
|
random number |
the exponential distribution is a special case of the gamma distribution: |
|
PROC specification |
gamma( |
gamma( |
density |
|
|
parameter restriction |
|
|
range |
|
same |
mean |
|
|
variance |
|
|
mode |
|
|
random number |
see (McGrath and Irving; 1973) |
|
PROC specification |
geo( |
density 1 |
|
parameter restriction |
|
range |
|
mean |
round( |
variance |
|
mode |
|
random number |
based on samples obtained from a Bernoulli distribution with probability |
PROC specification |
ichisq( |
density |
|
parameter restriction |
|
range |
|
mean |
|
variance |
|
mode |
|
random number |
inverse |
PROC specification |
igamma( |
igamma( |
density |
|
|
parameter restriction |
|
|
range |
|
same |
mean |
|
|
variance |
|
|
mode |
|
|
random number |
generate |
|
relationship to the gamma distribution |
|
|
PROC specification |
laplace( |
laplace( |
density |
|
|
parameter restriction |
|
|
range |
|
same |
mean |
|
|
variance |
|
|
mode |
|
|
random number |
inverse CDF. |
|
PROC specification |
logistic( |
density |
|
parameter restriction |
|
range |
|
mean |
|
variance |
|
mode |
|
random number |
inverse CDF method with |
PROC specification |
lognormal( |
lognormal( |
lognormal( |
density |
|
|
|
parameter restriction |
|
|
|
range |
|
same |
same |
mean |
|
|
|
variance |
|
|
|
mode |
|
|
|
random number |
generate |
||
PROC specification |
negbin( |
density |
|
parameter restriction |
|
range |
|
mean |
round |
variance |
|
mode |
|
random number |
generate |
PROC specification |
normal( |
normal( |
normal( |
density |
|
|
|
parameter restriction |
|
|
|
range |
|
same |
same |
mean |
|
same |
same |
variance |
|
|
|
mode |
|
same |
same |
PROC specification |
pareto( |
density |
|
parameter restriction |
|
range |
|
mean |
|
variance |
|
mode |
|
random number |
inverse CDF method with |
useful transformation |
|
PROC specification |
poisson( |
density |
|
parameter restriction |
|
range |
|
mean |
|
variance |
|
mode |
round |
PROC specification |
sichisq( |
density |
|
parameter restriction |
|
range |
|
mean |
|
variance |
|
mode |
|
random number |
scaled inverse |
PROC specification |
t( |
t( |
t( |
density |
|
|
|
parm restriction |
|
|
|
range |
|
same |
same |
mean |
|
same |
same |
variance |
|
|
|
mode |
|
same |
same |
random number |
|
||
PROC specification |
uniform( |
density |
|
parameter restriction |
none |
range |
|
mean |
|
variance |
|
mode |
does not exist |
random number |
Mersenne Twister (Matsumoto and Kurita; 1992, 1994; Matsumoto and Nishimura; 1998) |
PROC specification |
wald( |
density |
|
parameter restriction |
|
range |
|
mean |
|
variance |
|
mode |
|
random number |
generate |
PROC specification |
weibull( |
density |
|
parameter restriction |
|
range |
|
mean |
|
variance |
|
mode |
|
random number |
inverse CDF method with |
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
 ,
, 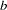 )
) 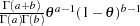
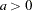 ,
, 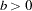

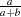
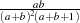
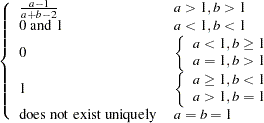
 , see
, see  , see
, see  and
and  , see
, see  or
or 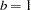 , inversion method; if
, inversion method; if  , uniform random variable
, uniform random variable  )
) 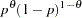

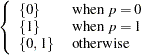

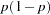
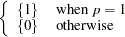
 . If
. If 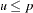 ,
,  ; else,
; else, 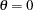
 ,
, 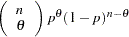

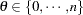
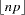
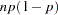
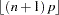
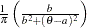


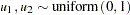 , let
, let 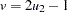 . Repeat the procedure until
. Repeat the procedure until 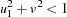 .
. 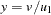 is a draw from the standard Cauchy, and
is a draw from the standard Cauchy, and 
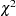 Distribution
Distribution )
) 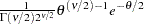
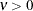
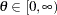 if
if 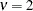 ;
; 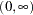 otherwise
otherwise 

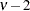 if
if  ; does not exist otherwise
; does not exist otherwise 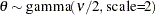 is a draw from the
is a draw from the 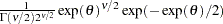
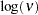
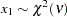 , and
, and  is a draw from the exponential
is a draw from the exponential 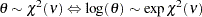
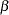 )
) 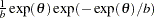

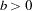
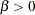

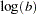
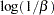
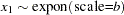 , and
, and 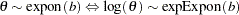

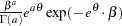
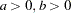

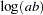
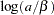
 , and
, and  distribution
distribution 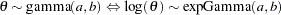
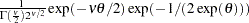
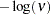
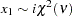 , and
, and 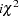 distribution
distribution 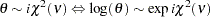

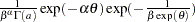
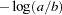

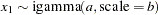 , and
, and 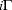 distribution
distribution 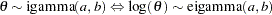
 )
) 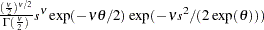
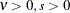
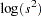
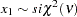 , and
, and 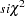 distribution
distribution 

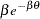
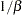
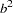
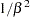
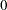
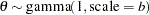 is a draw from the exponential distribution
is a draw from the exponential distribution 
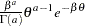
 if
if  otherwise
otherwise 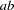

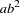
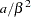
 if
if 
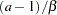 if
if 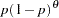


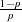 )
) 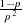
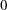
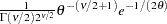
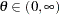
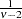 if
if 
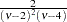 if
if 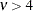
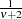
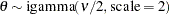 is a draw from the inverse
is a draw from the inverse 
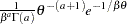
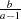 if
if 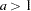
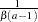 if
if 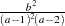


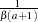
 is a draw from the
is a draw from the 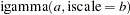 distribution
distribution 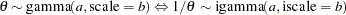
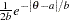
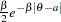
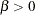
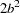
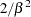
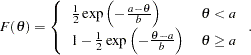 Generate
Generate 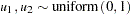 . If
. If 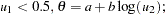 else
else 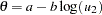 .
.  is a draw from the Laplace distribution
is a draw from the Laplace distribution 
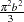
 . Generate
. Generate 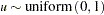 , and
, and 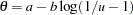 is a draw from the logistic distribution
is a draw from the logistic distribution 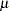 ,
,  )
)  )
) 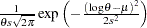
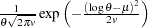
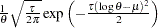

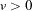

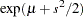
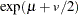

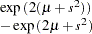
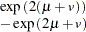
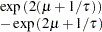
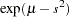

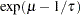
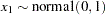 , and
, and  is a draw from the lognormal distribution
is a draw from the lognormal distribution 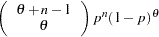
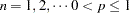

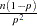

 , and
, and 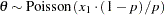
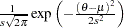
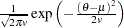

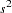
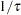
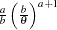

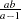 if
if 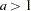
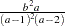
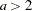
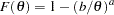 . Generate
. Generate 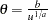 is a draw from the Pareto distribution.
is a draw from the Pareto distribution. 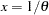 is Beta(
is Beta(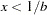 }.
}.  )
) 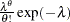
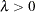
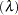
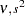 )
) 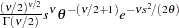
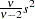 if
if 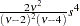 if
if 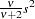
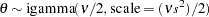 is a draw from the scaled inverse
is a draw from the scaled inverse 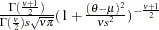
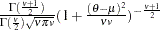
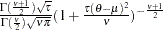
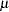 if
if 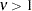
 if
if 
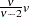 if
if 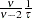 if
if 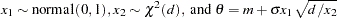 is a draw from the t-distribution.
is a draw from the t-distribution. 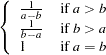
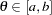
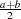

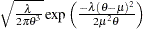
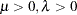

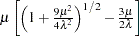
 . Let
. Let 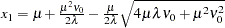 and
and  . Perform a Bernoulli trial,
. Perform a Bernoulli trial, 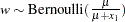 . If
. If 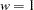 , choose
, choose 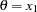 ; otherwise, choose
; otherwise, choose 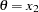
 ,
,  )
) 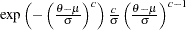
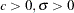
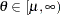 if
if  otherwise
otherwise 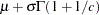
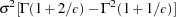
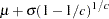 if
if 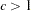
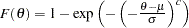 . Generate
. Generate 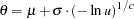 is a draw from the Weibull distribution.
is a draw from the Weibull distribution. 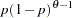 , which counts the total number of trials until the first success.
, which counts the total number of trials until the first success.