| The LIFETEST Procedure |
| STRATA Statement |
- STRATA variable <(list)> <...variable < (list)> > </options> ;
In the preceding syntax, variable is a variable whose values determine the stratum levels, and list is a list of endpoints for a numeric variable. The values for variable can be formatted or unformatted. If the variable is a character variable, or if the variable is numeric and no list appears, then the strata are defined by the unique values of the strata variable. More than one variable can be specified in the STRATA statement, and each numeric variable can be followed by a list. Each interval contains its lower endpoint but not its upper endpoint. The corresponding strata are formed by the combination of levels. If a variable is numeric and is followed by a list, then the levels for that variable correspond to the intervals defined by the list. The initial interval is assumed to start at  , and the final interval is assumed to end at
, and the final interval is assumed to end at  .
.
The specification of STRATA variables can have any of the following forms:
list separated by blanks |
strata age(5 10 20 30) |
|
list separated by commas |
strata age(5,10,20,30) |
|
x to y |
strata age(5 to 10) |
|
x to y by z |
strata age(5 to 30 by 10) |
|
combination of the above |
strata age(5,10 to 50 by 10) |
For example, the specification
strata Age(5,20 to 50 by 10) Sex;
indicates the following levels for the Age variable:
 |
This statement also specifies that the Age strata be further subdivided by values of the variable Sex. In this example, there are 6 age groups by 2 sex groups, forming a total of 12 strata.
The specification of several strata variables, such as
strata A B C;
is equivalent to the A*B*C syntax of the TABLES statement in the FREQ procedure. The number of strata levels usually grows very rapidly with the number of STRATA variables, so you must be cautious when specifying the list of STRATA variables.
When comparing more than two survival curves, a k-sample test tells you whether the curves are significantly different from each other, but it does not identify which pairs of curves are different. A multiple-comparison adjustment of the p-values for the paired comparisons retains the same overall false positives as the k-sample test. Two types of paired comparisons can be made: comparisons between all pairs of curves and comparisons between a control curve and all other curves. You use the DIFF= option to specify the comparison type, and you use the ADJUST= option to select a method of multiple-comparison adjustments.
Table 49.2 summaries the options available in the STRATA statement.
Option |
Description |
|---|---|
Homogeneity Tests |
|
specifies the group variable for stratified tests |
|
suppresses printing the test statistic and covariance matrix |
|
suppresses any tests |
|
specifies tests corresponding to various weight functions |
|
requests a trend test |
|
Multiple Comparisons |
|
requests a multiple-comparison adjustment |
|
specifies the type of differences to consider |
|
Missing Strata Value |
|
allows missing values as valid stratum values |
|
Options in the STRATA statement are specified after a slash ("/"). The following list describes these options.
- ADJUST=method
- specifies the multiple-comparison method for adjusting the p-values of the paired tests. See the section Multiple-Comparison Adjustments for mathematical details; also see Westfall et al. (1999). The adjustment methods include the following:
- BONFERRONI
- BON
- DUNNETT
performs Dunnett’s two-tailed comparisons of the control group with all other groups. PROC LIFETEST uses the factor-analytic covariance approximation described in Hsu (1992) and identifies the adjustment in the results as "Dunnett-Hsu." Note that ADJUST=DUNNETT is incompatible with DIFF=ALL.
- SCHEFFE
- SIDAK
- SMM
- GTE
performs the paired comparisons based on the studentized maximum modulus test.
- TUKEY
performs the paired comparisons based on Tukey’s studentized range test. PROC LIFETEST uses the approximation described in Kramer (1956) and identifies the adjustment as "Tukey-Kramer" in the results. Note that ADJUST=TUKEY is incompatible with DIFF=CONTROL.
- SIMULATE <(simulate-options)>
computes the adjusted p-values from the simulated distribution of the maximum or maximum absolute value of a multivariate normal random vector. The simulation estimates
 , the true
, the true 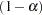 th quantile, where
th quantile, where  is the value of the ALPHA= simulate-option.
is the value of the ALPHA= simulate-option. The number of samples for the SIMULATE adjustment is set so that the tail area for the simulated
 is within a certain accuracy radius
is within a certain accuracy radius 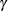 of
of  with an accuracy confidence of
with an accuracy confidence of 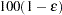 %. In equation form,
%. In equation form, 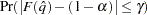


where
 is the simulated
is the simulated  and
and 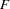 is the true distribution function of the maximum; see Edwards and Berry (1987) for details. By default,
is the true distribution function of the maximum; see Edwards and Berry (1987) for details. By default, 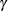 = 0.005 and
= 0.005 and  = 0.01 so that the tail area of
= 0.01 so that the tail area of  is within 0.005 of 0.95 with 99% confidence.
is within 0.005 of 0.95 with 99% confidence. The simulate-options include the following:
- ACC=value
specifies the target accuracy radius
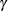 of a
of a 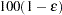 % confidence interval for the true probability content of the estimated
% confidence interval for the true probability content of the estimated 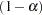 th quantile. The default value is ACC=0.005.
th quantile. The default value is ACC=0.005. - ALPHA=value
specifies the value
 for estimating the
for estimating the 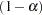 th quantile. The default value is the ALPHA= value in the PROC LIFETEST statement, or 0.05 if that option is not specified.
th quantile. The default value is the ALPHA= value in the PROC LIFETEST statement, or 0.05 if that option is not specified. - EPS=value
specifies the value
 for a
for a 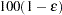 % confidence interval for the true probability content of the estimated
% confidence interval for the true probability content of the estimated 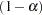 th quantile. The default value for the accuracy confidence is 99%, corresponding to EPS=0.01.
th quantile. The default value for the accuracy confidence is 99%, corresponding to EPS=0.01. - NSAMP=n
specifies the sample size for the simulation. By default,
 is set based on the values of the target accuracy radius
is set based on the values of the target accuracy radius 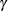 and accuracy confidence
and accuracy confidence 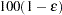 % for an interval for the true probability content of the estimated
% for an interval for the true probability content of the estimated 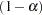 th quantile. With the default values for
th quantile. With the default values for 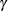 ,
,  , and
, and  (0.005, 0.01, and 0.05, respectively), NSAMP=12604 by default.
(0.005, 0.01, and 0.05, respectively), NSAMP=12604 by default. - REPORT
specifies that a report on the simulation should be displayed, including a listing of the parameters, such as
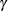 ,
,  , and
, and  , as well as an analysis of various methods for estimating or approximating the quantile.
, as well as an analysis of various methods for estimating or approximating the quantile. - SEED=number
specifies an integer used to start the pseudo-random number generator for the simulation. If you do not specify a seed, or if you specify a value less than or equal to zero, the seed is by default generated from reading the time of day from the computer’s clock.
- DIFF=ALL | CONTROL<(’string’ <..., ’string’>)>
- specifies which pairs of survival curves are considered for the multiple comparisons.
- DIFF=ALL
requests all paired comparisons
- DIFF=CONTROL <(’string’ <...’string’>)>
requests comparisons of the control curve with all other curves. To specify the control curve, you specify the quotes strings of formatted values that represent the curve in parentheses. For example, if Cell=’large’ identifies the control group, you specify
DIFF=CONTROL('large')If more than one variable is used to identify the curves (for example, if Cell=’large’ and Sex=’F’ represent the control), you specify
DIFF=CONTROL('large' 'F')The order of the quoted strings should correspond to the order of the stratum variables. If no specific curve is specified as the control, the first stratum or group value is used.
- GROUP=variable
specifies the variable whose formatted values identify the various samples whose underlying survival curves are to be compared. The tests are stratified on the levels of the STRATA variables. For instance, in a multicenter trial in which two forms of therapy are to be compared, you specify the variable identifying therapies as the GROUP= variable and the variable identifying centers as the STRATA variable, in order to perform a stratified test to compare the therapies while controlling the effect of the centers.
- MISSING
allows missing values to be a stratum level or a valid value of the GROUP= variable.
- NODETAIL
suppresses the display of the rank statistics and the corresponding covariance matrices for various strata. If the TREND option is specified, the display of the scores for computing the trend tests is suppressed.
- NOTEST
suppresses the k-sample tests, stratified tests, and trend tests.
- TREND
computes the trend tests for testing the null hypothesis that the
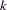 population hazards rate are the same versus an ordered alternatives. If there is only one STRATA variable and the variable is numeric, the unformatted values of the variable are used as the scores; otherwise, the scores are
population hazards rate are the same versus an ordered alternatives. If there is only one STRATA variable and the variable is numeric, the unformatted values of the variable are used as the scores; otherwise, the scores are 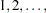 in the given order of the strata.
in the given order of the strata. - TEST=test-request
- TEST=(test-request <...test-request> )
controls the tests produced. Each test corresponds to a different weight function (see the section Nonparametric Tests for the weight functions). The test requests include the following:
- ALL
specifies all the nonparametric tests with
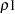 =1 and
=1 and 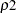 =0 for the Fleming and Harrington test—FLEMING(1,0).
=0 for the Fleming and Harrington test—FLEMING(1,0). - FLEMING(
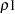 ,
, 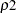 )
) specifies the family of tests in Harrington and Fleming (1982), where
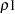 and
and 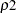 are nonnegative numbers. FLEMING(
are nonnegative numbers. FLEMING(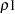 ,
,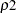 ) reduces to the Fleming-Harrington
) reduces to the Fleming-Harrington 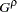 family (Fleming and Harrington; 1981) when
family (Fleming and Harrington; 1981) when 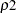 =0, which you can specify as FLEMING(
=0, which you can specify as FLEMING( ) with one argument. When
) with one argument. When  =0, the test becomes the log-rank test. When
=0, the test becomes the log-rank test. When  =1, the test should be very close to the Peto-Peto test.
=1, the test should be very close to the Peto-Peto test. - LOGRANK
- NONE
suppresses all comparison tests. Specifying TEST=NONE is equivalent to specify NOTEST.
- LR
specifies the likelihood ratio test based on the exponential model.
- MODPETO
- PETO
specifies the Peto-Peto test. The test is also referred to as the Peto-Peto-Prentice test.
- WILCOXON
specifies the Wilcoxon test. The test is also referred to as the Gehan test or the Breslow test.
- TARONE
By default, TEST=(LOGRANK WILCOXON LR) for the k-sample tests, and TEST=(LOGRANK WILCOXON) for stratified and trend tests.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
 idák correction to the raw p-values.
idák correction to the raw p-values.