| The LIFETEST Procedure |
Comparison of Two or More Groups of Survival Data
Let 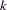 be the number of groups. Let
be the number of groups. Let 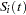 be the underlying survivor function
be the underlying survivor function  th group,
th group, 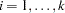 . The null and alternative hypotheses to be tested are
. The null and alternative hypotheses to be tested are
 for all
for all 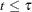
versus
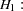 at least one of the
at least one of the 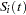 ’s is different for some
’s is different for some 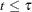
respectively, where  is the largest observed time.
is the largest observed time.
Likelihood Ratio Test
The likelihood ratio test statistic (Lawless; 1982) for test 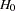 versus
versus 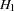 assumes that the data in the various samples are exponentially distributed and tests that the scale parameters are equal. The test statistic is computed as
assumes that the data in the various samples are exponentially distributed and tests that the scale parameters are equal. The test statistic is computed as
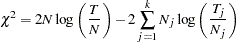 |
where 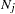 is the total number of events in the
is the total number of events in the  th stratum,
th stratum,  ,
, 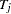 is the total time on test in the
is the total time on test in the  th stratum, and
th stratum, and 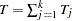 . The approximate probability value is computed by treating
. The approximate probability value is computed by treating  as having a chi-square distribution with
as having a chi-square distribution with 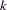 –1 degrees of freedom.
–1 degrees of freedom.
Nonparametric Tests
Let 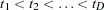 be the distinct event times in the pooled sample. At time
be the distinct event times in the pooled sample. At time 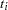 , let
, let  be a positive weight function, and let
be a positive weight function, and let 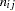 and
and 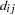 be the size of the risk set and the number of events in the
be the size of the risk set and the number of events in the  th sample, respectively. Let
th sample, respectively. Let  ,
, 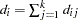 , and
, and 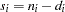 .
.
The choices of the weight function  are given in Table 49.3.
are given in Table 49.3.
Test |
|
|---|---|
log-rank |
1.0 |
Wilcoxon |
|
Tarone-Ware |
|
Peto-Peto |
|
modified Peto-Peto |
|
Harrington-Fleming ( |
|
where  is the product-limit estimate at
is the product-limit estimate at  for the pooled sample, and
for the pooled sample, and  is a survivor function estimate close to
is a survivor function estimate close to  given by
given by
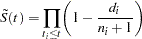 |
Unstratified Tests
The rank statistics (Klein and Moeschberger; 1997, Section 7.3) for testing 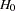 versus
versus 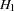 have the form of a
have the form of a 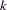 -vector
-vector 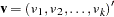 with
with
 |
and the estimated covariance matrix, 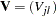 , is given by
, is given by
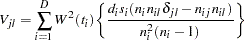 |
where 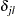 is 1 if
is 1 if 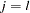 and 0 otherwise. The term
and 0 otherwise. The term  can be interpreted as a weighted sum of observed minus expected numbers of failure under the null hypothesis of identical survival curves. The overall test statistic for homogeneity is
can be interpreted as a weighted sum of observed minus expected numbers of failure under the null hypothesis of identical survival curves. The overall test statistic for homogeneity is 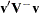 , where
, where 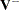 denotes a generalized inverse of
denotes a generalized inverse of 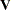 . This statistic is treated as having a chi-square distribution with degrees of freedom equal to the rank of
. This statistic is treated as having a chi-square distribution with degrees of freedom equal to the rank of 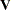 for the purposes of computing an approximate probability level.
for the purposes of computing an approximate probability level.
Stratified Tests
Suppose the test is to be stratified on 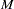 levels of a set of STRATA variables. Based only on the data of the
levels of a set of STRATA variables. Based only on the data of the  th stratum (
th stratum (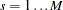 ), let
), let 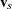 be the test statistic (Klein and Moeschberger; 1997, Section 7.5) for the
be the test statistic (Klein and Moeschberger; 1997, Section 7.5) for the  th stratum, and let
th stratum, and let  be its covariance matrix. Let
be its covariance matrix. Let
 |
 |
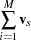 |
|||
 |
 |
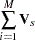 |
A global test statistic is constructed as
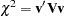 |
Under the null hypothesis, the test statistic has a  distribution with the same degrees of freedom as the individual test for each stratum.
distribution with the same degrees of freedom as the individual test for each stratum.
Multiple-Comparison Adjustments
Let 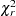 denote a chi-squared random variable with
denote a chi-squared random variable with  degrees of freedom. Denote
degrees of freedom. Denote  and
and 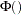 as the density function and the distribution function of a standard normal distribution, respectively. Let
as the density function and the distribution function of a standard normal distribution, respectively. Let 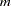 be the number of comparisons; that is,
be the number of comparisons; that is,
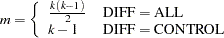 |
For a two-sided test comparing the survival of the  th group with that of
th group with that of 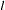 th group,
th group, 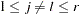 , the test statistic is
, the test statistic is
 |
and the raw p-value is
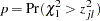 |
Adjusted p-values for various multiple-comparison adjustments are computed as follows:
- Bonferroni Adjustment
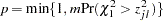
- Dunnett-Hsu Adjustment
With the first group being the control, let
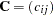 be the
be the 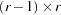 matrix of contrasts; that is,
matrix of contrasts; that is, 
Let
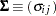 and
and 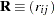 be covariance and correlation matrices of
be covariance and correlation matrices of 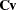 , respectively; that is,
, respectively; that is, 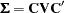
and
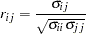
The factor-analytic covariance approximation of Hsu (1992) is to find
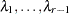 such that
such that 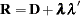
where
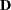 is a diagonal matrix with the
is a diagonal matrix with the  th diagonal element being
th diagonal element being 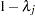 and
and 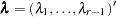 . The adjusted p-value is
. The adjusted p-value is 
which can be obtained in a DATA step as 1 – PROBMC("DUNNETT2",
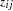 ,.,.,
,.,.,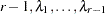 ).
). - Scheffé Adjustment
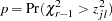
 idák Adjustment
idák Adjustment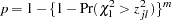
- SMM Adjustment
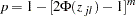
which can also be evaluated in a DATA step as 1 – PROBMC("MAXMOD",
 ).
). - Tukey Adjustment
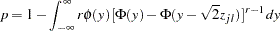
which can also be evaluated in a DATA step as 1 – PROBMC("RANGE",
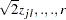 ).
).
Trend Tests
Trend tests (Klein and Moeschberger; 1997, Section 7.4) have more power to detect ordered alternatives as
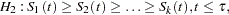 with at least one inequality
with at least one inequality
or
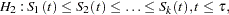 with at least one inequality
with at least one inequality
Let  be a sequence of scores associated with the
be a sequence of scores associated with the 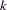 samples. The test statistic and its standard error are given by
samples. The test statistic and its standard error are given by  and
and 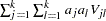 , respectively. Under
, respectively. Under 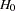 , the z-score
, the z-score
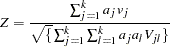 |
has, asymptotically, a standard normal distribution. PROC LIFETEST provides both one-tail and two-tail p-values for the test.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.

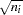
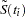
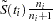
 ,
, )
)