PROC KRIGE2D: Investigating the Effect of Model Specification on Prediction :: SAS/STAT(R) 9.2 User's Guide, Second Edition

The KRIGE2D Procedure

Example 46.1 Investigating the Effect of Model Specification on Prediction

In the section Theoretical Semivariogram Model Fitting in the VARIOGRAM procedure, a particular theoretical semivariogram is chosen for the coal seam thickness data. The chosen semivariogram is Gaussian with a scale (sill) of 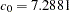$\text{[math]}$ , and a range of $\text{[math]}$ . This choice of the semivariogram is based on an automated fit by using PROC NLIN.

Another possible choice of model is the spherical semivariogram with the same scale (sill) of 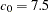$\text{[math]}$ but with a range of 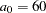$\text{[math]}$ . This choice of range comes from a visual fit, which is based on a comparison of the plots of the regular and robust sample semivariograms and the spherical semivariogram for various scale (sill) and range values. While not as good as the Gaussian model, the fit is reasonable.

It is generally held that spatial prediction is robust against model specification, while the standard error computation is not so robust.

This example investigates the effect of using these different models on the prediction and associated standard errors. First, you use a DATA step to input the thickness data as in the following:

   data thick;
      input East North Thick @@;
      label Thick='Coal Seam Thickness';
      datalines;
       0.7  59.6  34.1   2.1  82.7  42.2   4.7  75.1  39.5 
       4.8  52.8  34.3   5.9  67.1  37.0   6.0  35.7  35.9
       6.4  33.7  36.4   7.0  46.7  34.6   8.2  40.1  35.4   
      13.3   0.6  44.7  13.3  68.2  37.8  13.4  31.3  37.8
      17.8   6.9  43.9  20.1  66.3  37.7  22.7  87.6  42.8 
      23.0  93.9  43.6  24.3  73.0  39.3  24.8  15.1  42.3
      24.8  26.3  39.7  26.4  58.0  36.9  26.9  65.0  37.8 
      27.7  83.3  41.8  27.9  90.8  43.3  29.1  47.9  36.7
      29.5  89.4  43.0  30.1   6.1  43.6  30.8  12.1  42.8
      32.7  40.2  37.5  34.8   8.1  43.3  35.3  32.0  38.8
      37.0  70.3  39.2  38.2  77.9  40.7  38.9  23.3  40.5
      39.4  82.5  41.4  43.0   4.7  43.3  43.7   7.6  43.1
      46.4  84.1  41.5  46.7  10.6  42.6  49.9  22.1  40.7
      51.0  88.8  42.0  52.8  68.9  39.3  52.9  32.7  39.2
      55.5  92.9  42.2  56.0   1.6  42.7  60.6  75.2  40.1
      62.1  26.6  40.1  63.0  12.7  41.8  69.0  75.6  40.1
      70.5  83.7  40.9  70.9  11.0  41.7  71.5  29.5  39.8
      78.1  45.5  38.7  78.2   9.1  41.7  78.4  20.0  40.8
      80.5  55.9  38.7  81.1  51.0  38.6  83.8   7.9  41.6
      84.5  11.0  41.5  85.2  67.3  39.4  85.5  73.0  39.8 
      86.7  70.4  39.6  87.2  55.7  38.8  88.1   0.0  41.6
      88.4  12.1  41.3  88.4  99.6  41.2  88.8  82.9  40.5 
      88.9   6.2  41.5  90.6   7.0  41.5  90.7  49.6  38.9 
      91.5  55.4  39.0  92.9  46.8  39.1  93.4  70.9  39.7 
      55.8  50.5  38.1  96.2  84.3  40.3  98.2  58.2  39.5
      ;

You run the KRIGE2D procedure on the original Gaussian model, as the following statements show:

   proc krige2d data=thick outest=pred1 noprint;
      coordinates xc=East yc=North;
      predict var=Thick r=60;
      model scale=7.2881 range=30.6239 form=gauss;
      grid x=0 to 100 by 10 y=0 to 100 by 10;
   run;

Then, you run the KRIGE2D procedure by using a spherical model with a modified range, using the following statements:

   proc krige2d data=thick outest=pred2 noprint;
      coordinates xc=East yc=North;
      predict var=Thick r=60;
      model scale=7.5 range=60 form=spherical;
      grid x=0 to 100 by 10 y=0 to 100 by 10;
   run;

Eventually, you perform the comparison and obtain the comparison results by using the COMPARE and the PRINT procedures as the following statements show:

   data compare;
      merge pred1(rename=(estimate=g_prd stderr=g_std))
            pred2(rename=(estimate=s_prd stderr=s_std));
      prd_dif=g_prd-s_prd;
      std_dif=g_std-s_std;
   run;
   
   proc print data=compare;
      title 'Comparison of Gaussian and Spherical Models';
      title2 'Differences of Predictions and Standard Errors';
      var gxc gyc npoints g_prd s_prd prd_dif g_std s_std std_dif;
   run;

The predicted values at each of the grid locations do not differ greatly for the two semivariogram models. However, the standard error of prediction for the spherical model is substantially larger than for the Gaussian model. A partial outcome from the first 50 prediction grid points of the comparison analysis is shown in Output 46.1.1.

Output 46.1.1 Comparison of Gaussian and Spherical Models

Comparison of Gaussian and Spherical Models

Differences of Predictions and Standard Errors: First 50 Observations

Obs	GXC	GYC	NPOINTS	g_prd	s_prd	prd_dif	g_std	s_std	std_dif
1	0	0	23	43.9702	42.6700	1.30018	0.63046	2.05947	-1.42901
2	0	10	28	41.7145	41.6780	0.03657	0.50937	2.03464	-1.52526
3	0	20	31	38.9756	39.7285	-0.75291	0.27275	1.93478	-1.66203
4	0	30	33	36.1591	37.2816	-1.12253	0.11363	1.54521	-1.43157
5	0	40	40	33.8340	35.4018	-1.56771	0.04291	1.37653	-1.33361
6	0	50	39	32.8464	34.3835	-1.53711	0.02561	1.22559	-1.19997
7	0	60	36	33.9556	34.3140	-0.35842	0.00168	0.54120	-0.53952
8	0	70	31	36.9217	37.6517	-0.73009	0.03428	1.20363	-1.16935
9	0	80	31	41.1035	41.1016	0.00192	0.04180	0.99544	-0.95364
10	0	90	28	43.6723	42.5216	1.15068	0.09125	1.57357	-1.48232
11	0	100	23	41.8818	42.6511	-0.76939	0.48854	2.20792	-1.71938
12	10	0	25	44.6825	44.1959	0.48655	0.07061	1.09743	-1.02683
13	10	10	31	42.8441	42.7496	0.09449	0.09701	1.46686	-1.36984
14	10	20	35	40.3026	40.3557	-0.05301	0.04555	1.54876	-1.50321
15	10	30	40	37.7583	37.7659	-0.00754	0.00766	0.94135	-0.93369
16	10	40	45	35.6487	35.5495	0.09918	0.00497	0.75917	-0.75420
17	10	50	45	35.0798	34.7083	0.37154	0.01284	1.05027	-1.03743
18	10	60	42	36.0688	35.4784	0.59034	0.01123	1.18270	-1.17147
19	10	70	37	38.1205	38.1052	0.01527	0.00272	0.89156	-0.88884
20	10	80	34	41.2811	41.0803	0.20080	0.02097	1.22754	-1.20657
21	10	90	30	43.2213	42.8904	0.33089	0.05290	1.49438	-1.44148
22	10	100	26	40.9801	43.1350	-2.15488	0.17057	1.93434	-1.76377
23	20	0	29	44.4724	44.4359	0.03655	0.05490	1.23618	-1.18128
24	20	10	36	43.3401	43.2958	0.04428	0.00417	0.95510	-0.95092
25	20	20	40	41.1299	40.9923	0.13757	0.00547	1.18538	-1.17991
26	20	30	44	38.6046	38.5335	0.07118	0.00765	1.08968	-1.08203
27	20	40	50	36.5357	36.5331	0.00258	0.02509	1.33589	-1.31080
28	20	50	50	36.1273	35.8019	0.32543	0.02075	1.31950	-1.29875
29	20	60	50	36.8110	36.5435	0.26748	0.00684	1.11476	-1.10791
30	20	70	40	38.4321	38.5186	-0.08647	0.00217	0.89419	-0.89202
31	20	80	37	41.0639	41.0482	0.01561	0.00645	1.18542	-1.17898
32	20	90	34	43.1765	43.1070	0.06948	0.00524	0.94924	-0.94400
33	20	100	27	42.7637	43.4689	-0.70513	0.06070	1.52094	-1.46024
34	30	0	36	43.4020	43.9436	-0.54159	0.03891	1.32240	-1.28348
35	30	10	40	43.1542	43.1454	0.00879	0.00175	0.72412	-0.72237
36	30	20	45	41.2410	41.2158	0.02520	0.00397	1.10233	-1.09836
37	30	30	53	38.9347	39.0203	-0.08556	0.00391	1.04491	-1.04100
38	30	40	58	37.2798	37.3441	-0.06425	0.00654	0.89225	-0.88571
39	30	50	58	36.7224	36.7485	-0.02611	0.00534	0.83405	-0.82871
40	30	60	56	37.2079	37.3339	-0.12594	0.00561	1.00195	-0.99634
41	30	70	49	38.8800	38.8913	-0.01132	0.00225	1.01429	-1.01204
42	30	80	44	41.0573	41.0664	-0.00910	0.00192	0.97336	-0.97145
43	30	90	37	43.0975	43.0463	0.05114	0.00168	0.51312	-0.51144
44	30	100	30	44.6255	43.3247	1.30077	0.12062	1.57134	-1.45072
45	40	0	37	42.8223	43.5137	-0.69134	0.01588	1.25685	-1.24097
46	40	10	41	42.8953	42.9167	-0.02144	0.00247	0.95163	-0.94916
47	40	20	53	41.1033	41.1816	-0.07829	0.00154	0.96204	-0.96049
48	40	30	61	39.3295	39.2949	0.03453	0.00366	1.05527	-1.05161
49	40	40	68	38.1841	37.9297	0.25443	0.01252	1.27124	-1.25872
50	40	50	68	37.3330	37.4359	-0.10284	0.02764	1.44559	-1.41796

Top of Page