The HPMIXED procedure is designed to solve large mixed model problems by using sparse matrix techniques. A mixed model can be large in many ways: a large number of observations, a large number of columns in the 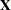matrix, a large number of columns in the matrix, and a large number of covariance parameters. The aim of the HPMIXED procedure is parameter estimation, inference, and prediction in linear mixed models with large 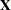and/or matrices and many observations, but with relatively few covariance parameters.

The models that you can fit with the HPMIXED procedure and the available postprocessing analyses are a subset of the models and analyses available with the MIXED procedure. With the HPMIXED procedure you can model only G-side random effects with variance component structure or an unstructured covariance matrix in a Cholesky parameterization. R-side random effects and direct modeling of their covariance structures are not supported.

The MIXED and HPMIXED procedures offer different balances for computing performance and statistical generality. To some extent the generality of the MIXED procedure means that it cannot serve as a high-performance computing tool for all of the model-data scenarios that it can potentially handle. For example, although efficient sparse algorithms are available to estimate variance components in large linear mixed models, the computational configuration changes profoundly when, for example, Kenward-Roger degree-of-freedom adjustments are requested.

On the other hand, the HPMIXED procedure can handle only a small subset of the models that PROC MIXED can fit. Invariably, some features of high-performance sparse computing methods might be surprising at first. For example, the best computational path depends on the model and the data, so that in models with a singular 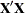matrix, the order in which singularities are detected and accounted for can change from one data set to the next.

The following is a list of features available in the MIXED procedure, but not available in the HPMIXED procedure:

• a REPEATED statement to model R-side covariance structures

• a variety of covariance structures by using the TYPE= option in the RANDOM statement

• automatic Type III tests of fixed effects. You request tests of fixed effects in the HPMIXED procedure with the TEST statement.

• ODS statistical graphics

• advanced degree-of-freedom adjustments available by using the DDFM= option

• maximum likelihood or method-of-moments estimation for the covariance parameters

• a PRIOR statement for a sampling-based Bayesian analysis