PROC GLM: Regression with Mileage Data :: SAS/STAT(R) 9.2 User's Guide, Second Edition

The GLM Procedure

Example 39.2 Regression with Mileage Data

A car is tested for gas mileage at various speeds to determine at what speed the car achieves the highest gas mileage. A quadratic model is fit to the experimental data. The following statements produce Output 39.2.1 through Output 39.2.4.

   title 'Gasoline Mileage Experiment';
   data mileage;
      input mph mpg @@;
      datalines;
   20 15.4
   30 20.2
   40 25.7
   50 26.2  50 26.6  50 27.4
   55   .
   60 24.8
   ;

   ods graphics on;
   proc glm;
      model mpg=mph mph*mph / p clm;
   run;
   ods graphics off;

Output 39.2.1 Standard Regression Analysis

Gasoline Mileage Experiment

The GLM Procedure

Number of Observations Read	8
Number of Observations Used	7

Gasoline Mileage Experiment

The GLM Procedure

Dependent Variable: mpg

Source	DF	Sum of Squares	Mean Square	F Value	Pr > F
Model	2	111.8086183	55.9043091	77.96	0.0006
Error	4	2.8685246	0.7171311
Corrected Total	6	114.6771429

R-Square	Coeff Var	Root MSE	mpg Mean
0.974986	3.564553	0.846836	23.75714

Source	DF	Type I SS	Mean Square	F Value	Pr > F
mph	1	85.64464286	85.64464286	119.43	0.0004
mph*mph	1	26.16397541	26.16397541	36.48	0.0038

Source	DF	Type III SS	Mean Square	F Value	Pr > F
mph	1	41.01171219	41.01171219	57.19	0.0016
mph*mph	1	26.16397541	26.16397541	36.48	0.0038

Parameter	Estimate	Standard Error	t Value	Pr > \|t\|
Intercept	-5.985245902	3.18522249	-1.88	0.1334
mph	1.305245902	0.17259876	7.56	0.0016
mph*mph	-0.013098361	0.00216852	-6.04	0.0038

The overall 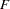$\text{[math]}$ statistic is significant. The tests of mph and mph*mph in the Type I sums of squares show that both the linear and quadratic terms in the regression model are significant. The model fits well, with an 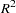$\text{[math]}$ of 0.97. The table of parameter estimates indicates that the estimated regression equation is

$\text{[math]}$

Output 39.2.2 Results of Requesting the P and CLM Options

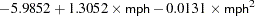Observation		Observed	Predicted	Residual	95% Confidence Limits for Mean Predicted Value
1		15.40000000	14.88032787	0.51967213	12.69701317	17.06364257
2		20.20000000	21.38360656	-1.18360656	20.01727192	22.74994119
3		25.70000000	25.26721311	0.43278689	23.87460041	26.65982582
4		26.20000000	26.53114754	-0.33114754	25.44573423	27.61656085
5		26.60000000	26.53114754	0.06885246	25.44573423	27.61656085
6		27.40000000	26.53114754	0.86885246	25.44573423	27.61656085
7	*	.	26.18073770	.	24.88679308	27.47468233
8		24.80000000	25.17540984	-0.37540984	23.05954977	27.29126990

The P and CLM options in the MODEL statement produce the table shown in Output 39.2.2. For each observation, the observed, predicted, and residual values are shown. In addition, the 95% confidence limits for a mean predicted value are shown for each observation. Note that the observation with a missing value for mph is not used in the analysis, but predicted and confidence limit values are shown.

Output 39.2.3 Additional Results of Requesting the P and CLM Options

Sum of Residuals	-0.00000000
Sum of Squared Residuals	2.86852459
Sum of Squared Residuals - Error SS	-0.00000000
PRESS Statistic	23.18107335
First Order Autocorrelation	-0.54376613
Durbin-Watson D	2.94425592

The last portion of the output listing, shown in Output 39.2.3, gives some additional information about the residuals. The Press statistic gives the sum of squares of predicted residual errors, as described in Chapter 4, Introduction to Regression Procedures. The First Order Autocorrelation and the Durbin-Watson 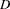$\text{[math]}$ statistic, which measures first-order autocorrelation, are also given.

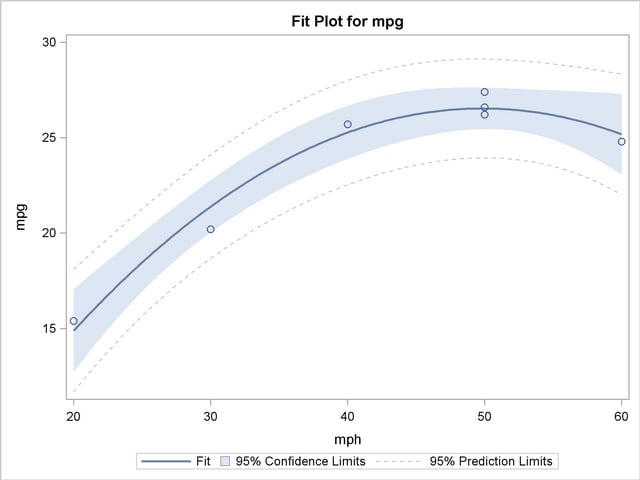
Output 39.2.4 Plot of Mileage Data

Finally, the ODS GRAPHICS ON command in the previous statements enables ODS Graphics, which in this case produces the plot shown in Output 39.2.4 of the actual and predicted values for the data, as well as a band representing the confidence limits for individual predictions. The quadratic relationship between mpg and mph is evident.

Top of Page