| The CLUSTER Procedure |
Example 29.3 Cluster Analysis of Fisher’s Iris Data
The iris data published by Fisher (1936) have been widely used for examples in discriminant analysis and cluster analysis. The sepal length, sepal width, petal length, and petal width are measured in millimeters on 50 iris specimens from each of three species, Iris setosa, I. versicolor, and I. virginica. Mezzich and Solomon (1980) discuss a variety of cluster analyses of the iris data.
The following code analyzes the iris data by using Ward’s method and two-stage density linkage and then illustrates how the FASTCLUS procedure can be used in combination with PROC CLUSTER to analyze large data sets.
title 'Cluster Analysis of Fisher (1936) Iris Data';
proc format;
value specname
1='Setosa '
2='Versicolor'
3='Virginica ';
run;
data iris;
input SepalLength SepalWidth PetalLength PetalWidth Species @@;
format Species specname.;
label SepalLength='Sepal Length in mm.'
SepalWidth ='Sepal Width in mm.'
PetalLength='Petal Length in mm.'
PetalWidth ='Petal Width in mm.';
symbol = put(species, specname10.);
datalines;
50 33 14 02 1 64 28 56 22 3 65 28 46 15 2 67 31 56 24 3
63 28 51 15 3 46 34 14 03 1 69 31 51 23 3 62 22 45 15 2
59 32 48 18 2 46 36 10 02 1 61 30 46 14 2 60 27 51 16 2
65 30 52 20 3 56 25 39 11 2 65 30 55 18 3 58 27 51 19 3
68 32 59 23 3 51 33 17 05 1 57 28 45 13 2 62 34 54 23 3
77 38 67 22 3 63 33 47 16 2 67 33 57 25 3 76 30 66 21 3
49 25 45 17 3 55 35 13 02 1 67 30 52 23 3 70 32 47 14 2
64 32 45 15 2 61 28 40 13 2 48 31 16 02 1 59 30 51 18 3
55 24 38 11 2 63 25 50 19 3 64 32 53 23 3 52 34 14 02 1
49 36 14 01 1 54 30 45 15 2 79 38 64 20 3 44 32 13 02 1
67 33 57 21 3 50 35 16 06 1 58 26 40 12 2 44 30 13 02 1
77 28 67 20 3 63 27 49 18 3 47 32 16 02 1 55 26 44 12 2
50 23 33 10 2 72 32 60 18 3 48 30 14 03 1 51 38 16 02 1
61 30 49 18 3 48 34 19 02 1 50 30 16 02 1 50 32 12 02 1
61 26 56 14 3 64 28 56 21 3 43 30 11 01 1 58 40 12 02 1
51 38 19 04 1 67 31 44 14 2 62 28 48 18 3 49 30 14 02 1
51 35 14 02 1 56 30 45 15 2 58 27 41 10 2 50 34 16 04 1
46 32 14 02 1 60 29 45 15 2 57 26 35 10 2 57 44 15 04 1
50 36 14 02 1 77 30 61 23 3 63 34 56 24 3 58 27 51 19 3
57 29 42 13 2 72 30 58 16 3 54 34 15 04 1 52 41 15 01 1
71 30 59 21 3 64 31 55 18 3 60 30 48 18 3 63 29 56 18 3
49 24 33 10 2 56 27 42 13 2 57 30 42 12 2 55 42 14 02 1
49 31 15 02 1 77 26 69 23 3 60 22 50 15 3 54 39 17 04 1
66 29 46 13 2 52 27 39 14 2 60 34 45 16 2 50 34 15 02 1
44 29 14 02 1 50 20 35 10 2 55 24 37 10 2 58 27 39 12 2
47 32 13 02 1 46 31 15 02 1 69 32 57 23 3 62 29 43 13 2
74 28 61 19 3 59 30 42 15 2 51 34 15 02 1 50 35 13 03 1
56 28 49 20 3 60 22 40 10 2 73 29 63 18 3 67 25 58 18 3
49 31 15 01 1 67 31 47 15 2 63 23 44 13 2 54 37 15 02 1
56 30 41 13 2 63 25 49 15 2 61 28 47 12 2 64 29 43 13 2
51 25 30 11 2 57 28 41 13 2 65 30 58 22 3 69 31 54 21 3
54 39 13 04 1 51 35 14 03 1 72 36 61 25 3 65 32 51 20 3
61 29 47 14 2 56 29 36 13 2 69 31 49 15 2 64 27 53 19 3
68 30 55 21 3 55 25 40 13 2 48 34 16 02 1 48 30 14 01 1
45 23 13 03 1 57 25 50 20 3 57 38 17 03 1 51 38 15 03 1
55 23 40 13 2 66 30 44 14 2 68 28 48 14 2 54 34 17 02 1
51 37 15 04 1 52 35 15 02 1 58 28 51 24 3 67 30 50 17 2
63 33 60 25 3 53 37 15 02 1
;
The following macro, SHOW, is used in the subsequent analyses to display cluster results. It invokes the FREQ procedure to crosstabulate clusters and species. The CANDISC procedure computes canonical variables for discriminating among the clusters, and the first two canonical variables are plotted to show cluster membership. See Chapter 27, The CANDISC Procedure, for a canonical discriminant analysis of the iris species.
/*--- Define macro show ---*/
%macro show;
proc freq;
tables cluster*species / nopercent norow nocol plot=none;
run;
proc candisc noprint out=can;
class cluster;
var petal: sepal:;
run;
proc sgplot data=can ;
scatter y=can2 x=can1 / group=cluster ;
run;
%mend;
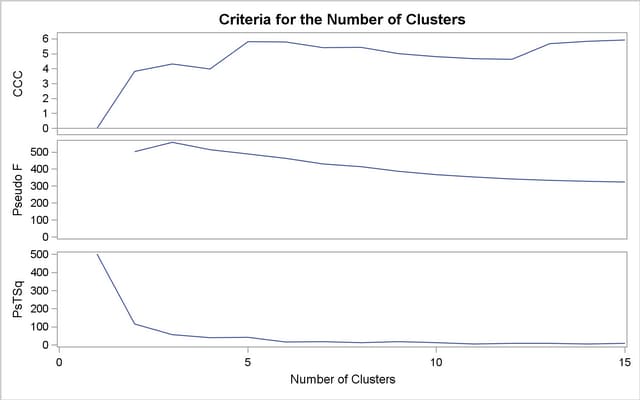
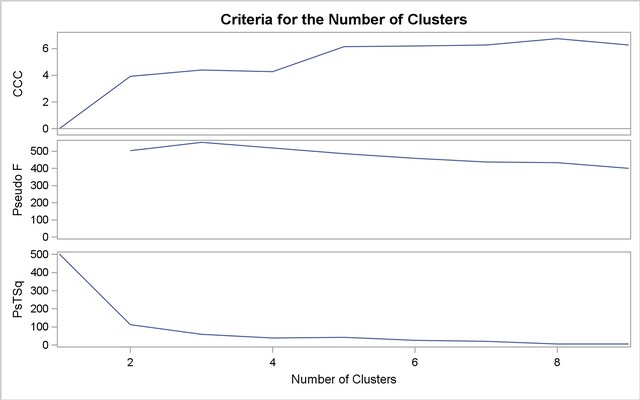
The first analysis clusters the iris data by using Ward’s method (see Output 29.3.1) and plots the CCC and pseudo 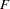 and
and 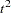 statistics (see Output 29.3.2). The CCC has a local peak at 3 clusters but a higher peak at 5 clusters. The pseudo
statistics (see Output 29.3.2). The CCC has a local peak at 3 clusters but a higher peak at 5 clusters. The pseudo 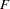 statistic indicates 3 clusters, while the pseudo
statistic indicates 3 clusters, while the pseudo 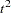 statistic suggests 3 or 6 clusters.
statistic suggests 3 or 6 clusters.
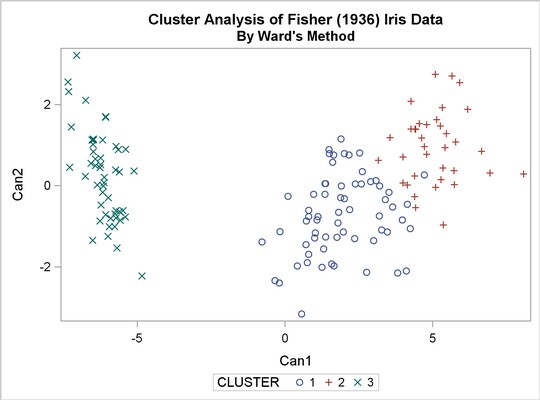
The TREE procedure creates an output data set containing the 3-cluster partition for use by the SHOW macro. The FREQ procedure reveals 16 misclassifications. The results are shown in Output 29.3.3.
title2 'By Ward''s Method';
ods graphics on ;
proc cluster data=iris method=ward print=15 ccc pseudo;
var petal: sepal:;
copy species;
run;
proc tree noprint ncl=3 out=out;
copy petal: sepal: species;
run;
%show;
| Eigenvalues of the Covariance Matrix | ||||
|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | |
| 1 | 422.824171 | 398.557096 | 0.9246 | 0.9246 |
| 2 | 24.267075 | 16.446125 | 0.0531 | 0.9777 |
| 3 | 7.820950 | 5.437441 | 0.0171 | 0.9948 |
| 4 | 2.383509 | 0.0052 | 1.0000 | |
| Cluster History | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NCL | Clusters Joined | FREQ | SPRSQ | RSQ | ERSQ | CCC | PSF | PST2 | T i e |
|
| 15 | CL24 | CL28 | 15 | 0.0016 | .971 | .958 | 5.93 | 324 | 9.8 | |
| 14 | CL21 | CL53 | 7 | 0.0019 | .969 | .955 | 5.85 | 329 | 5.1 | |
| 13 | CL18 | CL48 | 15 | 0.0023 | .967 | .953 | 5.69 | 334 | 8.9 | |
| 12 | CL16 | CL23 | 24 | 0.0023 | .965 | .950 | 4.63 | 342 | 9.6 | |
| 11 | CL14 | CL43 | 12 | 0.0025 | .962 | .946 | 4.67 | 353 | 5.8 | |
| 10 | CL26 | CL20 | 22 | 0.0027 | .959 | .942 | 4.81 | 368 | 12.9 | |
| 9 | CL27 | CL17 | 31 | 0.0031 | .956 | .936 | 5.02 | 387 | 17.8 | |
| 8 | CL35 | CL15 | 23 | 0.0031 | .953 | .930 | 5.44 | 414 | 13.8 | |
| 7 | CL10 | CL47 | 26 | 0.0058 | .947 | .921 | 5.43 | 430 | 19.1 | |
| 6 | CL8 | CL13 | 38 | 0.0060 | .941 | .911 | 5.81 | 463 | 16.3 | |
| 5 | CL9 | CL19 | 50 | 0.0105 | .931 | .895 | 5.82 | 488 | 43.2 | |
| 4 | CL12 | CL11 | 36 | 0.0172 | .914 | .872 | 3.99 | 515 | 41.0 | |
| 3 | CL6 | CL7 | 64 | 0.0301 | .884 | .827 | 4.33 | 558 | 57.2 | |
| 2 | CL4 | CL3 | 100 | 0.1110 | .773 | .697 | 3.83 | 503 | 116 | |
| 1 | CL5 | CL2 | 150 | 0.7726 | .000 | .000 | 0.00 | . | 503 | |
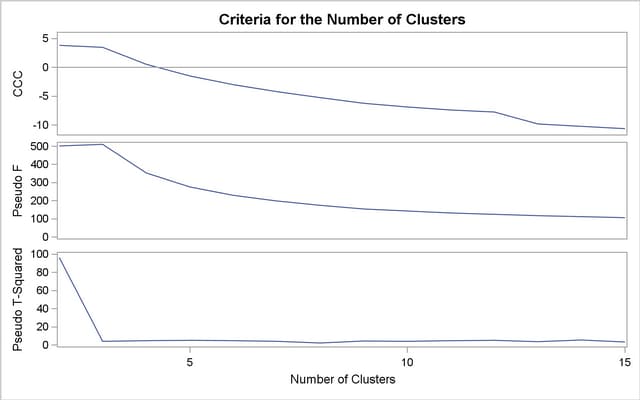
The second analysis uses two-stage density linkage. The raw data suggest 2 or 6 modes instead of 3:
|
modes |
|
3 |
12 |
|
4-6 |
6 |
|
7 |
4 |
|
8 |
3 |
|
9-50 |
2 |
|
51+ |
1 |
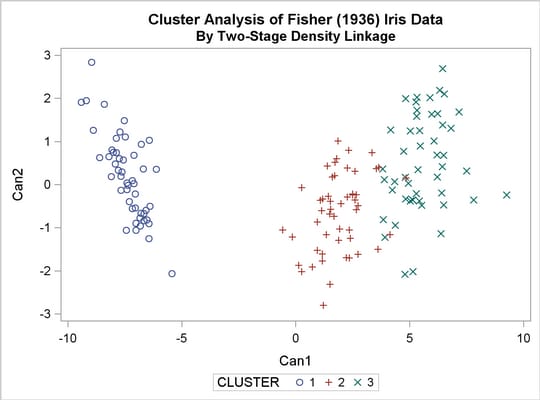
The following analysis uses K=8 to produce 3 clusters for comparison with other analyses. There are only 6 misclassifications. The results are shown in Output 29.3.5 and Output 29.3.6.
title2 'By Two-Stage Density Linkage';
ods graphics on ;
proc cluster data=iris method=twostage k=8 print=15 ccc pseudo;
var petal: sepal:;
copy species;
run;
proc tree noprint ncl=3 out=out;
copy petal: sepal: species;
run;
%show;
| Eigenvalues of the Covariance Matrix | ||||
|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | |
| 1 | 422.824171 | 398.557096 | 0.9246 | 0.9246 |
| 2 | 24.267075 | 16.446125 | 0.0531 | 0.9777 |
| 3 | 7.820950 | 5.437441 | 0.0171 | 0.9948 |
| 4 | 2.383509 | 0.0052 | 1.0000 | |
| Cluster History | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NCL | FREQ | SPRSQ | RSQ | ERSQ | CCC | PSF | PST2 | Normalized Fusion Density |
Maximum Density in Each Cluster |
T i e |
|||
| Clusters Joined | Lesser | Greater | |||||||||||
| 15 | CL17 | OB127 | 43 | 0.0024 | .917 | .958 | -11 | 107 | 3.4 | 0.3903 | 0.2066 | 3.5156 | |
| 14 | CL16 | OB137 | 50 | 0.0023 | .915 | .955 | -10 | 113 | 5.6 | 0.3637 | 0.1837 | 100.0 | |
| 13 | CL15 | OB74 | 44 | 0.0029 | .912 | .953 | -9.8 | 119 | 3.8 | 0.3553 | 0.2130 | 3.5156 | |
| 12 | CL22 | OB49 | 47 | 0.0036 | .909 | .950 | -7.7 | 125 | 5.2 | 0.3223 | 0.1736 | 8.3678 | T |
| 11 | CL12 | OB85 | 48 | 0.0036 | .905 | .946 | -7.4 | 132 | 4.8 | 0.3223 | 0.1736 | 8.3678 | |
| 10 | CL11 | OB98 | 49 | 0.0033 | .902 | .942 | -6.8 | 143 | 4.1 | 0.2879 | 0.1479 | 8.3678 | |
| 9 | CL13 | OB24 | 45 | 0.0036 | .898 | .936 | -6.2 | 155 | 4.5 | 0.2802 | 0.2005 | 3.5156 | |
| 8 | CL10 | OB25 | 50 | 0.0019 | .896 | .930 | -5.2 | 175 | 2.2 | 0.2699 | 0.1372 | 8.3678 | |
| 7 | CL8 | OB121 | 51 | 0.0035 | .893 | .921 | -4.2 | 198 | 4.0 | 0.2586 | 0.1372 | 8.3678 | |
| 6 | CL9 | OB45 | 46 | 0.0041 | .888 | .911 | -3.0 | 229 | 4.7 | 0.1412 | 0.0832 | 3.5156 | |
| 5 | CL6 | OB39 | 47 | 0.0048 | .884 | .895 | -1.5 | 276 | 5.1 | 0.107 | 0.0605 | 3.5156 | |
| 4 | CL5 | OB21 | 48 | 0.0048 | .879 | .872 | 0.54 | 353 | 4.7 | 0.0969 | 0.0541 | 3.5156 | |
| 3 | CL4 | OB90 | 49 | 0.0046 | .874 | .827 | 3.49 | 511 | 4.2 | 0.0715 | 0.0370 | 3.5156 | |
| 2 | CL7 | CL3 | 100 | 0.1017 | .773 | .697 | 3.83 | 503 | 96.3 | 2.6277 | 3.5156 | 8.3678 | |
The CLUSTER procedure is not practical for very large data sets because, with most methods, the CPU time is roughly proportional to the square or cube of the number of observations. The FASTCLUS procedure requires time proportional to the number of observations and can therefore be used with much larger data sets than PROC CLUSTER. If you want to hierarchically cluster a very large data set, you can use PROC FASTCLUS for a preliminary cluster analysis to produce a large number of clusters and then use PROC CLUSTER to hierarchically cluster the preliminary clusters.
FASTCLUS automatically creates the variables _FREQ_ and _RMSSTD_ in the MEAN= output data set. These variables are then automatically used by PROC CLUSTER in the computation of various statistics.
The following SAS code uses the iris data to illustrate the process of clustering clusters. In the preliminary analysis, PROC FASTCLUS produces 10 clusters, which are then crosstabulated with species. The data set containing the preliminary clusters is sorted in preparation for later merges. The results are shown in Output 29.3.9 and Output 29.3.10.
title2 'Preliminary Analysis by FASTCLUS';
proc fastclus data=iris summary maxc=10 maxiter=99 converge=0
mean=mean out=prelim cluster=preclus;
var petal: sepal:;
run;
proc freq;
tables preclus*species / nopercent norow nocol plot=none;
run;
proc sort data=prelim;
by preclus;
run;
| Convergence criterion is satisfied. |
| Cluster Summary | ||||||
|---|---|---|---|---|---|---|
| Cluster | Frequency | RMS Std Deviation | Maximum Distance from Seed to Observation |
Radius Exceeded |
Nearest Cluster | Distance Between Cluster Centroids |
| 1 | 9 | 2.7067 | 8.2027 | 5 | 8.7362 | |
| 2 | 19 | 2.2001 | 7.7340 | 4 | 6.2243 | |
| 3 | 18 | 2.1496 | 6.2173 | 8 | 7.5049 | |
| 4 | 4 | 2.5249 | 5.3268 | 2 | 6.2243 | |
| 5 | 3 | 2.7234 | 5.8214 | 1 | 8.7362 | |
| 6 | 7 | 2.2939 | 5.1508 | 2 | 9.3318 | |
| 7 | 17 | 2.0274 | 6.9576 | 10 | 7.9503 | |
| 8 | 18 | 2.2628 | 7.1135 | 3 | 7.5049 | |
| 9 | 22 | 2.2666 | 7.5029 | 8 | 9.0090 | |
| 10 | 33 | 2.0594 | 10.0033 | 7 | 7.9503 | |
| Cluster Analysis of Fisher (1936) Iris Data |
| Preliminary Analysis by FASTCLUS |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
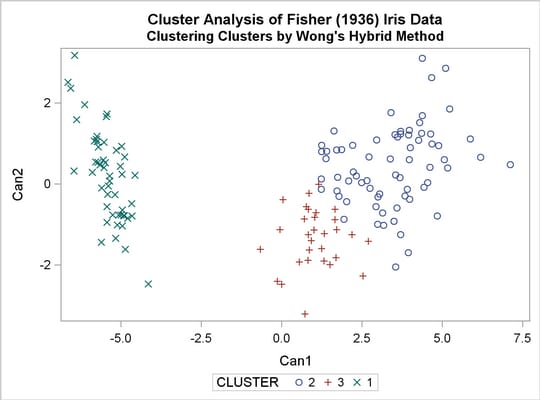
The following macro, CLUS, clusters the preliminary clusters. There is one argument to choose the METHOD= specification to be used by PROC CLUSTER. The TREE procedure creates an output data set containing the 3-cluster partition, which is sorted and merged with the OUT= data set from PROC FASTCLUS to determine which cluster each of the original 150 observations belongs to. The SHOW macro is then used to display the results. In this example, the CLUS macro is invoked using Ward’s method, which produces 16 misclassifications, and Wong’s hybrid method, which produces 22 misclassifications.
/*--- Define macro clus ---*/
%macro clus(method);
proc cluster data=mean method=&method ccc pseudo;
var petal: sepal:;
copy preclus;
run;
proc tree noprint ncl=3 out=out;
copy petal: sepal: preclus;
run;
proc sort data=out;
by preclus;
run;
data clus;
merge out prelim;
by preclus;
run;
%show;
%mend;
The following statements produce Output 29.3.11 through Output 29.3.14.
title2 'Clustering Clusters by Ward''s Method'; %clus(ward);
| Eigenvalues of the Covariance Matrix | ||||
|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | |
| 1 | 416.976349 | 398.666421 | 0.9501 | 0.9501 |
| 2 | 18.309928 | 14.952922 | 0.0417 | 0.9918 |
| 3 | 3.357006 | 3.126943 | 0.0076 | 0.9995 |
| 4 | 0.230063 | 0.0005 | 1.0000 | |
| Cluster History | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NCL | Clusters Joined | FREQ | SPRSQ | RSQ | ERSQ | CCC | PSF | PST2 | T i e |
|
| 9 | OB2 | OB4 | 23 | 0.0019 | .958 | .932 | 6.26 | 400 | 6.3 | |
| 8 | OB1 | OB5 | 12 | 0.0025 | .955 | .926 | 6.75 | 434 | 5.8 | |
| 7 | CL9 | OB6 | 30 | 0.0069 | .948 | .918 | 6.28 | 438 | 19.5 | |
| 6 | OB3 | OB8 | 36 | 0.0074 | .941 | .907 | 6.21 | 459 | 26.0 | |
| 5 | OB7 | OB10 | 50 | 0.0104 | .931 | .892 | 6.15 | 485 | 42.2 | |
| 4 | CL8 | OB9 | 34 | 0.0162 | .914 | .870 | 4.28 | 519 | 39.3 | |
| 3 | CL7 | CL6 | 66 | 0.0318 | .883 | .824 | 4.39 | 552 | 59.7 | |
| 2 | CL4 | CL3 | 100 | 0.1099 | .773 | .695 | 3.94 | 503 | 113 | |
| 1 | CL2 | CL5 | 150 | 0.7726 | .000 | .000 | 0.00 | . | 503 | |
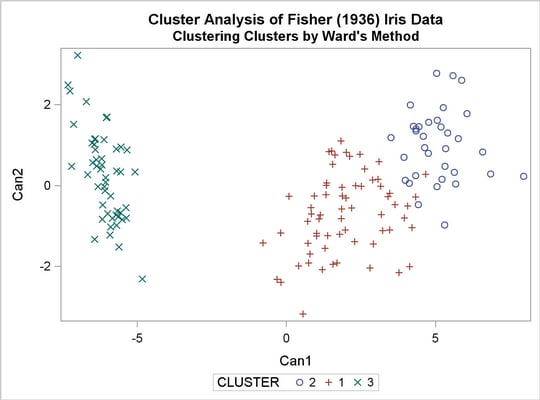
The following statements produce Output 29.3.15 through Output 29.3.17.
title2 "Clustering Clusters by Wong's Hybrid Method"; %clus(twostage hybrid);
| Eigenvalues of the Covariance Matrix | ||||
|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | |
| 1 | 416.976349 | 398.666421 | 0.9501 | 0.9501 |
| 2 | 18.309928 | 14.952922 | 0.0417 | 0.9918 |
| 3 | 3.357006 | 3.126943 | 0.0076 | 0.9995 |
| 4 | 0.230063 | 0.0005 | 1.0000 | |
| Cluster History | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NCL | FREQ | SPRSQ | RSQ | ERSQ | CCC | PSF | PST2 | Normalized Fusion Density |
Maximum Density in Each Cluster |
T i e |
|||
| Clusters Joined | Lesser | Greater | |||||||||||
| 9 | OB10 | OB7 | 50 | 0.0104 | .949 | .932 | 3.81 | 330 | 42.2 | 40.24 | 58.2179 | 100.0 | |
| 8 | OB3 | OB8 | 36 | 0.0074 | .942 | .926 | 3.22 | 329 | 26.0 | 27.981 | 39.4511 | 48.4350 | |
| 7 | OB2 | OB4 | 23 | 0.0019 | .940 | .918 | 4.24 | 373 | 6.3 | 23.775 | 8.9675 | 46.3026 | |
| 6 | CL8 | OB9 | 58 | 0.0194 | .921 | .907 | 2.13 | 334 | 46.3 | 20.724 | 46.8846 | 48.4350 | |
| 5 | CL7 | OB6 | 30 | 0.0069 | .914 | .892 | 3.09 | 383 | 19.5 | 13.303 | 17.6360 | 46.3026 | |
| 4 | CL6 | OB1 | 67 | 0.0292 | .884 | .870 | 1.21 | 372 | 41.0 | 8.4137 | 10.8758 | 48.4350 | |
| 3 | CL4 | OB5 | 70 | 0.0138 | .871 | .824 | 3.33 | 494 | 12.3 | 5.1855 | 6.2890 | 48.4350 | |
| 2 | CL3 | CL5 | 100 | 0.0979 | .773 | .695 | 3.94 | 503 | 89.5 | 19.513 | 46.3026 | 48.4350 | |
| 1 | CL2 | CL9 | 150 | 0.7726 | .000 | .000 | 0.00 | . | 503 | 1.3337 | 48.4350 | 100.0 | |
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
