| The CATMOD Procedure |
Example 28.1 Linear Response Function, r=2 Responses
In an example from Ries and Smith (1963), the choice of detergent brand (Brand M or X) is related to three other categorical variables: the softness of the laundry water (Softness
M or X) is related to three other categorical variables: the softness of the laundry water (Softness soft, medium, or hard), the temperature of the water (Temperature
soft, medium, or hard), the temperature of the water (Temperature high or low), and whether the subject was a previous user of Brand M (Previous
high or low), and whether the subject was a previous user of Brand M (Previous yes or no). The linear response function, which could also be specified as RESPONSE MARGINALS, yields one probability, Pr(brand preference=M), as the response function to be analyzed. Two models are fit in this example: the first model is a saturated one, containing all of the main effects and interactions, while the second is a reduced model containing only the main effects. The following statements produce Output 28.1.1 through Output 28.1.4:
yes or no). The linear response function, which could also be specified as RESPONSE MARGINALS, yields one probability, Pr(brand preference=M), as the response function to be analyzed. Two models are fit in this example: the first model is a saturated one, containing all of the main effects and interactions, while the second is a reduced model containing only the main effects. The following statements produce Output 28.1.1 through Output 28.1.4:
data detergent;
input Softness $ Brand $ Previous $ Temperature $ Count @@;
datalines;
soft X yes high 19 soft X yes low 57
soft X no high 29 soft X no low 63
soft M yes high 29 soft M yes low 49
soft M no high 27 soft M no low 53
med X yes high 23 med X yes low 47
med X no high 33 med X no low 66
med M yes high 47 med M yes low 55
med M no high 23 med M no low 50
hard X yes high 24 hard X yes low 37
hard X no high 42 hard X no low 68
hard M yes high 43 hard M yes low 52
hard M no high 30 hard M no low 42
;
title 'Detergent Preference Study';
proc catmod data=detergent;
response 1 0;
weight Count;
model Brand=Softness|Previous|Temperature / freq prob;
title2 'Saturated Model';
run;
The "Data Summary" table (Output 28.1.1) indicates that you have two response levels and twelve populations.
| Data Summary | |||
|---|---|---|---|
| Response | Brand | Response Levels | 2 |
| Weight Variable | Count | Populations | 12 |
| Data Set | DETERGENT | Total Frequency | 1008 |
| Frequency Missing | 0 | Observations | 24 |
The "Population Profiles" table in Output 28.1.2 displays the ordering of independent variable levels as used in the table of parameter estimates.
Since Brand M is the first level in the "Response Profiles" table (Output 28.1.3), the RESPONSE statement causes Pr(Brand=M) to be the single response function modeled.
The "Analysis of Variance" table in Output 28.1.4 shows that all of the interactions are nonsignificant.
| Analysis of Variance | |||
|---|---|---|---|
| Source | DF | Chi-Square | Pr > ChiSq |
| Intercept | 1 | 983.13 | <.0001 |
| Softness | 2 | 0.09 | 0.9575 |
| Previous | 1 | 22.68 | <.0001 |
| Softness*Previous | 2 | 3.85 | 0.1457 |
| Temperature | 1 | 3.67 | 0.0555 |
| Softness*Temperature | 2 | 0.23 | 0.8914 |
| Previous*Temperature | 1 | 2.26 | 0.1324 |
| Softnes*Previou*Temperat | 2 | 0.76 | 0.6850 |
| Residual | 0 | . | . |
Therefore, a main-effects model is fit with the following statements:
model Brand=Softness Previous Temperature
/ clparm noprofile design;
title2 'Main-Effects Model';
run;
quit;
The PROC CATMOD statement is not required due to the interactive capability of the CATMOD procedure. The NOPROFILE option suppresses the redisplay of the "Response Profiles" table. The CLPARM option produces 95% confidence limits for the parameter estimates. Output 28.1.5 through Output 28.1.7 are produced.
The design matrix in Output 28.1.5 displays the results of the differential-effects modeling used in PROC CATMOD.
| Data Summary | |||
|---|---|---|---|
| Response | Brand | Response Levels | 2 |
| Weight Variable | Count | Populations | 12 |
| Data Set | DETERGENT | Total Frequency | 1008 |
| Frequency Missing | 0 | Observations | 24 |
| Response Functions and Design Matrix | ||||||
|---|---|---|---|---|---|---|
| Sample | Response Function |
Design Matrix | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | 0.41667 | 1 | 1 | 0 | 1 | 1 |
| 2 | 0.38182 | 1 | 1 | 0 | 1 | -1 |
| 3 | 0.64179 | 1 | 1 | 0 | -1 | 1 |
| 4 | 0.58427 | 1 | 1 | 0 | -1 | -1 |
| 5 | 0.41071 | 1 | 0 | 1 | 1 | 1 |
| 6 | 0.43103 | 1 | 0 | 1 | 1 | -1 |
| 7 | 0.67143 | 1 | 0 | 1 | -1 | 1 |
| 8 | 0.53922 | 1 | 0 | 1 | -1 | -1 |
| 9 | 0.48214 | 1 | -1 | -1 | 1 | 1 |
| 10 | 0.45690 | 1 | -1 | -1 | 1 | -1 |
| 11 | 0.60417 | 1 | -1 | -1 | -1 | 1 |
| 12 | 0.46226 | 1 | -1 | -1 | -1 | -1 |
The analysis of variance table in Output 28.1.6 shows that previous use of Brand M, together with the temperature of the laundry water, is a significant factor in whether a subject prefers Brand M laundry detergent. The table also shows that the additive model fits since the goodness-of-fit statistic (the residual chi-square) is nonsignificant.
The chi-square test in Output 28.1.7 shows that the Softness parameters are not significantly different from zero; as expected, the Wald confidence limits for these two estimates contain zero. So softness of the water is not a factor in choosing Brand M.
| Analysis of Weighted Least Squares Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | Estimate | Standard Error |
Chi- Square |
Pr > ChiSq | 95% Confidence Limits | ||
| Intercept | 0.5080 | 0.0160 | 1004.93 | <.0001 | 0.4766 | 0.5394 | |
| Softness | hard | -0.00256 | 0.0218 | 0.01 | 0.9066 | -0.0454 | 0.0402 |
| med | 0.0104 | 0.0218 | 0.23 | 0.6342 | -0.0323 | 0.0530 | |
| Previous | no | -0.0711 | 0.0155 | 20.96 | <.0001 | -0.1015 | -0.0407 |
| Temperature | high | 0.0319 | 0.0161 | 3.95 | 0.0468 | 0.000446 | 0.0634 |
The negative coefficient for Previous (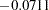 ) indicates that the first level of Previous (which is shown to be 'no') is associated with a smaller probability of preferring Brand M than the second level of Previous (with coefficient constrained to be 0.0711 since the parameter estimates for a given effect must sum to zero). In other words, previous users of Brand M are much more likely to prefer it than those who have never used it before.
) indicates that the first level of Previous (which is shown to be 'no') is associated with a smaller probability of preferring Brand M than the second level of Previous (with coefficient constrained to be 0.0711 since the parameter estimates for a given effect must sum to zero). In other words, previous users of Brand M are much more likely to prefer it than those who have never used it before.
Similarly, the positive coefficient for Temperature indicates that the first level of Temperature (which, from the "Population Profiles" table, is 'high') has a larger probability of preferring Brand M than the second level of Temperature. In other words, those who do their laundry in hot water are more likely to prefer Brand M than those who do their laundry in cold water.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.