 |
 |
Example 25.5 Ordinal Relations among Factor Loadings
The same data set as in Example 25.4 is used in McDonald (1980) for analysis with ordinally constrained factor loadings. In Example 25.4, the results of the linearly constrained factor analysis show that the loadings of the two factors are ordered as 2, 1, 3, 4, 6, 5. McDonald (1980) then tests the hypothesis that the factor loadings are all nonnegative and can be ordered in the following manner:
In this example, these ordinal relationships are implemented using the LINCON statement in the following COSAN model specification:
proc calis data=Kinzer method=max nobs=326 nose;
cosan D(6,DIA) * B(2,Gen) * I(2,Ide) + D(6,DIA) * PSI(6,DIA);
matrix B
[ ,1]= 0. b21 b31 b41 b51 b61,
[ ,2]= b12 b22 b32 b42 b52 b62;
matrix Psi
[1,1]= psi1-psi6;
matrix D
[1,1]= d1-d6 (6 * 1.);
lincon b21 <= b31,
b31 <= b41,
b41 <= b51,
b51 <= b61,
b62 <= b52,
b52 <= b42,
b42 <= b32,
b32 <= b22,
b22 <= b12;
bounds b21 >= 0;
/* SAS Programming Statements */
/* 6 Constraints on Correlation structures */
psi1 = 1. - b12 * b12;
psi2 = 1. - b21 * b21 - b22 * b22;
psi3 = 1. - b31 * b31 - b32 * b32;
psi4 = 1. - b41 * b41 - b42 * b42;
psi5 = 1. - b51 * b51 - b52 * b52;
psi6 = 1. - b61 * b61 - b62 * b62;
vnames D var1-var6,
B Fact1 Fact2,
I Fact1 Fact2,
Psi var1-var6;
run;
Again, as in Example 25.4, correlation structures are analyzed in the current example so that the error variance parameters psi1-psi6 are defined as functions of the loadings in the SAS programming statements. However, the loading parameters are not constrained the same way as in Example 25.4. First, b11 is fixed at  for identification purposes. Then, the LINCON statement is used to specify the ordinal relations of the factor loadings. Parameter b21 is set to be nonnegative in the BOUNDS statement.
for identification purposes. Then, the LINCON statement is used to specify the ordinal relations of the factor loadings. Parameter b21 is set to be nonnegative in the BOUNDS statement.
As shown in Output 25.5.1, the solution converges in 10 iterations. In the fit summary table, the chi-square test statistic is  (
(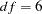 ,
, 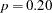 ). This indicates a good fit. However, in the model there are 11 loading parameters (the b’s) and 6 population standard deviation parameters (the d’s). The degrees of freedom should have been
). This indicates a good fit. However, in the model there are 11 loading parameters (the b’s) and 6 population standard deviation parameters (the d’s). The degrees of freedom should have been  , but why is this number 6 in the fit summary table?
, but why is this number 6 in the fit summary table?
Output 25.5.1
Final Iteration Status and Fit
| 10 |
13 |
| 11 |
2 |
| 0.0260990149 |
6.2794755E-6 |
| 0 |
0.9491590286 |
| 0.0001243346 |
|
| ABSGCONV convergence criterion satisfied. |
|
Warning: |
There are 2 active constraints at the solution. The standard errors and Chi-Square test statistic assume the solution is located in the interior of the parameter space and hence do not apply if it is likely that some different set of inequality constraints could be active. |
|
Note: |
The degrees of freedom are increased by the number of active constraints (see Dijkstra, 1992). The number of parameters in calculating fit indices is decreased by the number of active constraints. To turn off the adjustment, use the NOADJDF option. |
| 0.0261 |
| 0.9914 |
| 0.9699 |
| 0.0169 |
| 0.0169 |
| 0.3966 |
| 8.4822 |
| 6 |
| 0.2049 |
| 682.87 |
| 15 |
| 0.0357 |
| . |
| 0.0860 |
| 0.1204 |
| . |
| 0.1576 |
| 0.6154 |
| 0.9963 |
| 8.4575 |
| -3.5178 |
| -32.2392 |
| -26.2392 |
| 0.9962 |
| 0.9907 |
| 0.9876 |
| 0.3950 |
| 0.8281 |
| 0.9689 |
| 0.9963 |
| 484 |
The reason is that there are two active constraints in the solution, making it two free parameters fewer in the final solution than originally specified. Active constraints are those inequality constraints that are fulfilled on the boundary equalities. As shown in the "Optimization Results" table, the number of active constraints for the current fitting is two. The default treatment in PROC CALIS is to treat these active constraints as if they were going to happen for all possible repeated sampling. This might as well be seen as fitting the active equality constraints on every possible repeated samples. This results in an increase of the degrees of freedom for model fit, as adjusted in the current fit summary table in Output 25.5.1. To warn you about the degrees-of-freedom adjustment, the following messages are also printed with the output:
WARNING: There are 2 active constraints at the solution. The
standard errors and Chi-Square test statistic assume
solution is located in the interior of the parameter
space and hence do not apply if it is likely that some
different set of inequality constraints could be
active.
NOTE: The degrees of freedom are increased by the number of
active constraints (see Dijkstra, 1992). The number of
parameters in calculating fit indices is decreased by the
number of active constraints. To turn off the adjustment,
use the NOADJDF option.
When active constraints are encountered, you need to be cautious about two implications. First, the estimates fall on the boundary of the parameter space originally specified. As shown in Output 25.5.2, estimates for b51 and b61 are the same, and so are the pair of estimates for b12 and b22. These pairs of parameters were originally constrained by inequalities in the model. For example, b61 was constrained to be at least as big as b51. The fact that this constraint is honored only on the bound means that a better model fit might exist with b61 being smaller than b51. Similarly, a better model fit might result without requiring b12 to be at least as big as b22. Solutions with active constraints thus might imply that the original strict inequality constraints are not appropriate for the data.
The second implication for the presence of active constraints is that the chi-square test statistic and the standard error estimates are computed as if repeated samples were fitted by the model with the presence of the active equality constraints. The degrees-of-freedom adjustment by PROC CALIS is based on this assumption. However, if the presence of particular active constraints in fitting reflects only a rare sampling event that is not likely to happen in repeated sampling, degrees-of-freedom adjustment or even the computation of chi-square statistic and standard error estimates might not be justified. Unfortunately, whether the active constraints are reflecting the truth of the model or pure sampling fluctuation is usually difficult to determine.
Copyright
© 2009 by SAS Institute Inc., Cary, NC, USA. All
rights reserved.
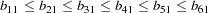
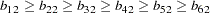
 for identification purposes. Then, the LINCON statement is used to specify the ordinal relations of the factor loadings. Parameter b21 is set to be nonnegative in the BOUNDS statement.
for identification purposes. Then, the LINCON statement is used to specify the ordinal relations of the factor loadings. Parameter b21 is set to be nonnegative in the BOUNDS statement.  (
(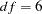 ,
, 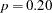 ). This indicates a good fit. However, in the model there are 11 loading parameters (the b’s) and 6 population standard deviation parameters (the d’s). The degrees of freedom should have been
). This indicates a good fit. However, in the model there are 11 loading parameters (the b’s) and 6 population standard deviation parameters (the d’s). The degrees of freedom should have been  , but why is this number 6 in the fit summary table?
, but why is this number 6 in the fit summary table?