| The CALIS Procedure |
| Computational Problems |
First Iteration Overflows
Analyzing a covariance matrix including high variances in the diagonal and using bad initial estimates for the parameters can easily lead to arithmetic overflows in the first iterations of the minimization algorithm. The line-search algorithms that work with cubic extrapolation are especially sensitive to arithmetic overflows. If this occurs with quasi-Newton or conjugate gradient minimization, you can specify the INSTEP= option to reduce the length of the first step. If an arithmetic overflow occurs in the first iteration of the Levenberg-Marquardt algorithm, you can specify the INSTEP= option to reduce the trust-region radius of the first iteration. You also can change the minimization technique or the line-search method. If none of these help, you should consider the following:
scaling the covariance matrix
providing better initial values
changing the model
No Convergence of Minimization Process
If convergence does not occur during the minimization process, perform the following tasks.
If there are negative variance estimates in the diagonal locations of the central model matrices, you can do the following:
Specify the BOUNDS statement to obtain nonnegative variance estimates.
Specify the HEYWOOD option, if the FACTOR model statement is specified.
Change the estimation method to obtain a better set of initial estimates. For example, if you use METHOD=ML, you can do the following:
Change to METHOD=LSML.
Run some iterations with METHOD=DWLS or METHOD=GLS, write the results in an OUTRAM= data set, and use the results as initial values specified by an INRAM= data set in a second run with METHOD=ML.
Change the optimization technique. For example, if you use the default TECH=LEVMAR, you can do the following:
Change to TECH=QUANEW or TECH=NEWRAP.
Run some iterations with TECH=CONGRA, write the results in an OUTRAM= data set, and use the results as initial values specified by an INRAM= data set in a second run with a different TECH= technique.
Change or modify the update technique or the line-search algorithm, or both, when using TECH=QUANEW or TECH=CONGRA. For example, if you use the default update formula and the default line-search algorithm, you can do the following:
Change the update formula with the UPDATE= option.
Change the line-search algorithm with the LIS= option.
Specify a more precise line search with the LSPRECISION= option, if you use LIS=2 or LIS=3.
Add more iterations and function calls by using the MAXIT= and MAXFU= options.
Change the initial values. For many categories of model specifications done by the LINEQS, RAM, or FACTOR model, PROC CALIS computes an appropriate set of initial values automatically. However, for some of the model specifications (for example, structural equations with latent variables on the left-hand side and manifest variables on the right-hand side), PROC CALIS can generate very obscure initial values. In these cases, you have to set the initial values yourself.
Increase the initial values of the parameters located at the diagonal of central matrices in one of the following ways:
manually, by setting the values in the model specification
automatically, by using the DEMPHAS= option
Use a slightly different, but more stable, model to obtain preliminary estimates.
Use additional information to specify initial values, such as by using other SAS software like the FACTOR, REG, SYSLIN, and MODEL (SYSNLIN) procedures for the modified, unrestricted model case.
Unidentified Model
The parameter vector  in the covariance structure model
in the covariance structure model
 |
is said to be identified in a parameter space  , if
, if
 |
implies  . The parameter estimates that result from an unidentified model can be very far from the parameter estimates of a very similar but identified model. They are usually machine dependent. Do not use parameter estimates of an unidentified model as initial values for another run of PROC CALIS.
. The parameter estimates that result from an unidentified model can be very far from the parameter estimates of a very similar but identified model. They are usually machine dependent. Do not use parameter estimates of an unidentified model as initial values for another run of PROC CALIS.
Singular Predicted Model Matrix
You can easily specify models with singular predicted model matrices, such as by fixing diagonal elements of central matrices to 0. In such cases, you cannot compute maximum likelihood estimates (the ML function value 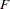 is not defined). Since singular predicted model matrices can also occur temporarily in the minimization process, PROC CALIS tries in such cases to change the parameter estimates so that the predicted model matrix becomes positive-definite. In such cases, the following message is displayed:
is not defined). Since singular predicted model matrices can also occur temporarily in the minimization process, PROC CALIS tries in such cases to change the parameter estimates so that the predicted model matrix becomes positive-definite. In such cases, the following message is displayed:
NOTE: Parameter set changed.
This process does not always work well, especially if there are fixed instead of variable diagonal elements in the central model matrices. A famous example where you cannot compute ML estimates is a component analysis with fewer components than given manifest variables. See the section FACTOR Model Statement for more details. If you continue to get a singular predicted model matrix after changing initial values and optimization techniques, then your model is perhaps specified so that ML estimates cannot be computed.
Saving Computing Time
For large models, the most computing time is needed to compute the modification indices. If you do not really need the Lagrange multipliers or multiple Wald test indices (the univariate Wald test indices are the same as the  values), using the NOMOD option can save a considerable amount of computing time.
values), using the NOMOD option can save a considerable amount of computing time.
Central Matrices with Negative Eigenvalues
A covariance matrix cannot have negative eigenvalues, since a negative eigenvalue means that some linear combination of the variables has negative variance. PROC CALIS displays a warning if a central model matrix has negative eigenvalues but does not actually compute the eigenvalues. Sometimes this warning can be triggered by 0 or very small positive eigenvalues that appear negative because of numerical error. If you want to be sure that the central model matrix you are fitting can be considered to be a variance-covariance matrix, you can use the SAS/IML command VAL=EIGVAL(U) to compute the vector VAL of eigenvalues of matrix 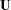 .
.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
 Values
Values of the endogenous variables are computed using the estimated error variances
of the endogenous variables are computed using the estimated error variances 
 , which results in
, which results in 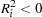 .
.