| The CALIS Procedure |
| FACTOR Model Statement |
You can use the FACTOR statement to specify an exploratory or confirmatory first-order factor analysis of the given covariance or correlation matrix 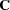 ,
,
 |
or
 |
where  is a diagonal matrix and
is a diagonal matrix and 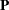 is symmetric. Within this section,
is symmetric. Within this section,  denotes the number of manifest variables corresponding to the rows and columns of matrix
denotes the number of manifest variables corresponding to the rows and columns of matrix 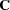 , and
, and 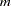 denotes the number of latent variables (factors or components) corresponding to the columns of the loading matrix
denotes the number of latent variables (factors or components) corresponding to the columns of the loading matrix  .
.
You can specify only one FACTOR statement with each PROC CALIS statement. You can specify higher-order factor analysis problems by using a COSAN model specification. PROC CALIS requires more computing time and memory than PROC FACTOR because it is designed for more general structural estimation problems and is unable to exploit the special properties of the unconstrained factor analysis model.
For default (exploratory) factor analysis, PROC CALIS computes initial estimates for factor loadings and unique variances by an algebraic method of approximate factor analysis. If you use a MATRIX statement together with a FACTOR model specification, initial values are computed by McDonald’s (McDonald and Hartmann 1992) method (if possible). For details, see Using the FACTOR and MATRIX Statements. If neither of the two methods is appropriate, the initial values are set by the START= option.
The unrestricted factor analysis model is not identified because any orthogonal rotated factor loading matrix  is equivalent to the result
is equivalent to the result  ,
,
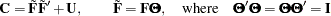 |
To obtain an identified factor solution, the FACTOR statement imposes zero constraints on the 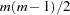 elements in the upper triangle of
elements in the upper triangle of  by default.
by default.
The following options are available in the FACTOR statement.
- COMPONENT | COMP
computes a component analysis instead of a factor analysis (the diagonal matrix
 in the model is set to 0). Note that the rank of
in the model is set to 0). Note that the rank of  is equal to the number
is equal to the number 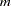 of components in
of components in  . If
. If 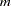 is smaller than the number of variables in the moment matrix
is smaller than the number of variables in the moment matrix 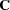 , the matrix of predicted model values is singular and maximum likelihood estimates for
, the matrix of predicted model values is singular and maximum likelihood estimates for  cannot be computed. You should compute ULS estimates in this case.
cannot be computed. You should compute ULS estimates in this case. - HEYWOOD | HEY
constrains the diagonal elements of
 to be nonnegative; in other words, the model is replaced by
to be nonnegative; in other words, the model is replaced by 
- N=m
specifies the number of first-order factors or components. The number
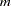 of factors should not exceed the number
of factors should not exceed the number  of variables in the covariance or correlation matrix analyzed. For the saturated model,
of variables in the covariance or correlation matrix analyzed. For the saturated model,  , the COMP option should generally be specified for
, the COMP option should generally be specified for 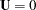 ; otherwise,
; otherwise,  . For
. For 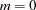 no factor loadings are estimated, and the model is
no factor loadings are estimated, and the model is  , with
, with  . By default,
. By default, 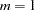 .
. - NORM <= KAISER | NONE>
Kaiser-normalizes the rows of the factor pattern for rotation. NORM=KAISER, which is the default, has exactly the same effect as NORM. You can turn off the normalization by NORM=NONE.
- RCONVERGE=p
- RCONV=p
specifies the convergence criterion for rotation cycles. The option is applicable to rotation by using either the QUARTIMAX, VARIMAX, EQUAMAX, or PARSIMAX method in the ROTATE= option. Rotation stops when the scaled change of the simplicity function value is less than the RCONVERGE= value. The default convergence criterion is

where
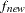 and
and  are simplicity function values of the current cycle and the previous cycle, respectively,
are simplicity function values of the current cycle and the previous cycle, respectively,  is a scaling factor, and
is a scaling factor, and  is 1E–9 by default and is modified by the RCONVERGE= value.
is 1E–9 by default and is modified by the RCONVERGE= value. - RITER=n
specifies the maximum number of cycles
 for factor rotation by using either the QUARTIMAX, VARIMAX, EQUAMAX, or PARSIMAX method in the ROTATE= option. The default
for factor rotation by using either the QUARTIMAX, VARIMAX, EQUAMAX, or PARSIMAX method in the ROTATE= option. The default  is the maximum between 10 times the number of variables and 100.
is the maximum between 10 times the number of variables and 100. - ROTATE | R=name
specifies an orthogonal rotation. By default, ROTATE=NONE. The possible values for name are as follows:
- PRINCIPAL | PC
specifies a principal axis rotation. If ROTATE=PRINCIPAL is used with a factor rather than a component model, the following rotation is performed:

where the columns of matrix
 contain the eigenvectors of
contain the eigenvectors of  .
. - QUARTIMAX | Q
specifies quartimax rotation.
- VARIMAX | V
specifies varimax rotation.
- EQUAMAX | E
specifies equamax rotation.
- PARSIMAX | P
specifies parsimax rotation.
- NONE
performs no rotation (default).
Using the FACTOR and MATRIX Statements
You can specify the MATRIX statement and the FACTOR statement to compute a confirmatory first-order factor or component analysis. You can define the elements of the matrices  ,
, 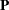 , and
, and  of the oblique model,
of the oblique model,
 |
To specify the structure for matrix  ,
, 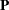 , or
, or  , you have to refer to the matrix _F_ , _P_ , or _U_ in the MATRIX statement. Matrix names automatically set by PROC CALIS always start with an underscore. As you name your own matrices or variables, you should avoid leading underscores.
, you have to refer to the matrix _F_ , _P_ , or _U_ in the MATRIX statement. Matrix names automatically set by PROC CALIS always start with an underscore. As you name your own matrices or variables, you should avoid leading underscores.
The default matrix forms are as follows:
- _F_
lower triangular matrix (0 upper triangle for problem identification, removing rotational invariance)
- _P_
identity matrix (constant)
- _U_
diagonal matrix
For details about specifying the elements in matrices, see the section MATRIX Statement. If you are using at least one MATRIX statement in connection with a FACTOR model statement, you can also use the BOUNDS or PARAMETERS statement and programming statements to constrain the parameters named in the MATRIX statement. Initial estimates are computed by McDonald’s (McDonald and Hartmann 1992) method. McDonald’s method of computing initial values works better if you scale the factors by setting the factor variances to 1 rather than by setting the loadings of the reference variables equal to 1.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.