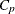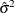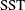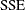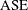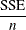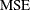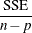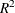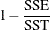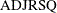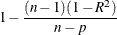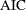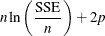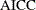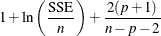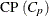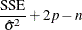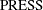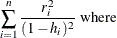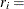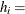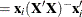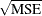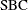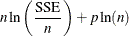The HPREG Procedure

Criteria Used in Model Selection

The HPREG procedure supports a variety of fit statistics that you can specify as criteria for the CHOOSE= , SELECT= , and STOP= options in the SELECTION statement. The following statistics are available:

ADJRSQ

Adjusted R-square statistic (Darlington 1968; Judge et al. 1985)

AIC

Akaike’s information criterion (Akaike 1969; Judge et al. 1985)

AICC

Corrected Akaike’s information criterion (Hurvich and Tsai 1989)

BIC | SBC

Schwarz Bayesian information criterion (Schwarz 1978; Judge et al. 1985)

CP

Mallows $C_ p$ statistic (Mallows 1973; Hocking 1976)

PRESS

Predicted residual sum of squares statistic

RSQUARE

R-square statistic (Darlington 1968; Judge et al. 1985)

SL

Significance used to assess an effect’s contribution to the fit when it is added to or removed from a model

VALIDATE

Average square error over the validation data

When you use SL as a criterion for effect selection, the definition depends on whether an effect is being considered as a drop or an add candidate. If the current model has p parameters excluding the intercept, and if you denote its residual sum of squares by 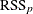$\mbox{RSS}_ p$ and you add an effect with k degrees of freedom and denote the residual sum of squares of the resulting model by 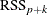$\mbox{RSS}_{p+k}$, then the F statistic for entry with k numerator degrees of freedom and 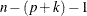$n-(p+k)-1$ denominator degrees of freedom is given by

\[ F= \frac{ (\mbox{RSS}_ p-\mbox{RSS}_{p+k})/k }{\mbox{RSS}_{p+k}/(n-(p+k)-1)} \]

where n is number of observations used in the analysis. The significance level for entry is the p-value of this F statistic, and is deemed significant if it is smaller than the SLENTRY limit. Among several such add candidates, the effect with the smallest p-value (most significant) is deemed best.

If you drop an effect with k degrees of freedom and denote the residual sum of squares of the resulting model by 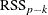$\mbox{RSS}_{p-k}$, then the F statistic for removal with k numerator degrees of freedom and 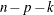$n-p-k$ denominator degrees of freedom is given by

\[ F= \frac{ (\mbox{RSS}_{p-k}-\mbox{RSS}_ p)/k }{\mbox{RSS}_ p/(n-p-k)} \]

where n is number of observations used in the analysis. The significance level for removal is the p-value of this F statistic, and the effect is deemed not significant if this p-value is larger than the SLSTAY limit. Among several such removal candidates, the effect with the largest p-value (least significant) is deemed the best removal candidate.

It is known that the "F-to-enter" and "F-to-delete" statistics do not follow an F distribution (Draper, Guttman, and Kanemasu 1971).. Hence the SLENTRY and SLSTAY values cannot reliably be viewed as probabilities. One way to address this difficulty is to replace hypothesis testing as a means of selecting a model with information criteria or out-of-sample prediction criteria. While Harrell (2001) points out that information criteria were developed for comparing only prespecified models, Burnham and Anderson (2002) note that AIC criteria have routinely been used for several decades for performing model selection in time series analysis.

Table 15.5 provides formulas and definitions for these fit statistics.

Table 15.5: Formulas and Definitions for Model Fit Summary Statistics

Statistic

Definition or Formula

n

Number of observations

p

Number of parameters including the intercept

$\hat{\sigma }^2$

Estimate of pure error variance from fitting the full model

$\mbox{SST}$

Total sum of squares corrected for the mean for the
dependent variable

$\mbox{SSE}$

Error sum of squares

$\mbox{ASE}$

$\displaystyle \frac{\mbox{SSE}}{n}$

$\mbox{MSE}$

$\displaystyle \frac{\mbox{SSE}}{n-p}$

$R^2 $

$1 - \displaystyle \frac{\mbox{SSE}}{\mbox{SST}} $

$\mbox{ADJRSQ}$

$1 - \displaystyle \frac{(n-1)(1-R^2)}{n-p}$

$\mbox{AIC} $

$\displaystyle n \ln \left( \frac{\mbox{SSE}}{n} \right) + 2p$

$\mbox{AICC} $

$\displaystyle 1 + \ln \left( \frac{\mbox{SSE}}{n} \right) + \frac{2(p+1)}{n-p-2} $

$\mbox{CP } (C_ p)$

$\displaystyle \frac{\mbox{SSE}}{\hat{\sigma }^2} + 2p - n$

$\mbox{PRESS}$

$\displaystyle \sum _{i=1}^ n \frac{r_ i^2}{(1-h_ i)^2}\mbox{ where } $
$r_ i = $ residual at observation i and
$h_ i = $ leverage of observation i $ = \mb{x}_ i(\mb{X}’\mb{X})^{-}\mb{x}_ i’$

$\mbox{RMSE}$

$\sqrt {\mbox{MSE}}$

$\mbox{SBC}$

$\displaystyle n \ln \left( \frac{\mbox{SSE}}{n} \right) + p \ln (n) $