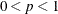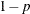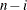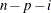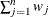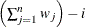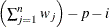-
COVARIANCE
COV
-
computes the principal components from the covariance matrix. If you omit the COV option, the correlation matrix is analyzed.
The COV option causes variables that have large variances to be more strongly associated with components that have large eigenvalues,
and it causes variables that have small variances to be more strongly associated with components that have small eigenvalues.
You should not specify the COV option unless the units in which the variables are measured are comparable or the variables
are standardized in some way.
-
DATA=SAS-data-set
-
specifies the SAS data set to be analyzed. The data set can only be an ordinary SAS data set (raw data). If you omit the DATA=
option, the HPPRINCOMP procedure uses the most recently created SAS data set.
If PROC HPPRINCOMP executes in distributed mode, the input data are distributed to memory on the appliance nodes and analyzed
in parallel, unless the data are already distributed in the appliance database. In that case PROC HPPRINCOMP reads the data
alongside the distributed database. For more information about the various execution modes, see the section Processing Modes. For more information about the alongside-the-database model, see the section Alongside-the-Database Execution.
-
METHOD=EIG | ITERGS<(iter-options)> | NIPALS<(iter-options)>
-
specifies the principal component extraction method to be used. You can specify the following values:
-
EIG
-
requests eigenvalue decomposition.
-
ITERGS<(iter-options)>
-
requests the iterative method based on Gram-Schmidt orthogonalization (ITERGS) of Andrecut (2009). You can also specify the following optional iter-options in parentheses after METHOD=ITERGS:
-
EPSILON=n
-
specifies the convergence criterion for the iterative method. By default, EPSILON=10E–12.
-
MAXITER=n
-
specifies the maximum number of iterations for the iterative method. By default, MAXITER=5000.
-
NOCENTER
-
suppresses centering of the numeric variables to be analyzed. This option is useful if the analysis variables are already
centered and scaled.
-
NOSCALE
-
suppresses scaling of the numeric variables to be analyzed. This option is useful if the analysis variables are already centered
and scaled.
-
NIPALS<(iter-options)>
-
requests the nonlinear iterative partial least squares (NIPALS) method. You can also specify the optional iter-options in parentheses after METHOD=NIPALS.
By default, METHOD=EIG. If you specify METHOD=NIPALS or METHOD=ITERGS, the following options in the PROC HPPRINCOMP
statement are ignored: COV, NOINT, OUT=, OUTSTAT=, PARPREFIX=, SINGULAR=, and STD.
-
N=number
-
specifies the number of principal components to be computed. The default is the number of variables. The value of the N= option
must be an integer greater than or equal to 0.
-
NOINT
-
omits the intercept from the model. In other words, the NOINT option requests that the covariance or correlation matrix not
be corrected for the mean. When you specify the NOINT option in the HPPRINCOMP procedure, the covariance matrix and, hence,
the standard deviations are not corrected for the mean. If you want to obtain the standard deviations corrected for the mean,
you can obtain them by using a procedure such as PROC MEANS.
If you use the NOINT option and also create an OUTSTAT= data set, the data set is TYPE=UCORR or TYPE=UCOV rather than TYPE=CORR
or TYPE=COV.
-
NOPRINT
-
suppresses the display of all output. This option temporarily disables the Output Delivery System (ODS). For more information,
see Chapter 20: Using the Output Delivery System in SAS/STAT 14.1 User's Guide.
-
OUT=SAS-data-set
-
creates an output SAS data set to contain observationwise principal component scores. To avoid data duplication when you have
large data sets, the variables in the input data set are not included in the output data set; however, variables that are specified in the ID
statement are included.
If the input data are in distributed form, in which access of data in a particular order cannot be guaranteed, the HPPRINCOMP
procedure copies the distribution or partition key to the output data set so that its contents can be joined with the input
data.
If you want to create a SAS data set in a permanent library, you must specify a two-level name. For more information about
permanent libraries and SAS data sets, see
SAS Language Reference: Concepts. For more information about OUT= data sets, see the section Output Data Sets.
-
OUTSTAT=SAS-data-set
-
creates an output SAS data set to contain means, standard deviations, number of observations, correlations or covariances,
eigenvalues, and eigenvectors. If you specify the COV option, the data set is TYPE=COV or TYPE=UCOV, depending on the NOINT
option, and it contains covariances; otherwise, the data set is TYPE=CORR or TYPE=UCORR, depending on the NOINT option, and
it contains correlations. If you specify the PARTIAL statement, the OUTSTAT= data set also contains R squares.
If you want to create a SAS data set in a permanent library, you must specify a two-level name. For more information about
permanent libraries and SAS data sets, see
SAS Language Reference: Concepts. For more information about OUTSTAT= data sets, see the section Output Data Sets.
-
PREFIX=name
-
specifies a prefix for naming the principal components. By default, the names are Prin1, Prin2, …, Prinn. If you specify PREFIX=Abc, the components are named Abc1, Abc2, Abc3, and so on. The number of characters in the prefix plus the number of digits required to designate the variables should not
exceed the current name length that is defined by the VALIDVARNAME= system option.
-
PARPREFIX=name
PPREFIX=name
RPREFIX=name
-
specifies a prefix for naming the residual variables in the OUT= data set and the OUTSTAT= data set. By default, the prefix
is R_. The number of characters in the prefix plus the maximum length of the variable names should not exceed the current name
length that is defined by the VALIDVARNAME= system option.
-
SINGULAR=p
SING=p
-
specifies the singularity criterion, where 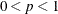 . If a variable in a PARTIAL statement has an R square as large as
. If a variable in a PARTIAL statement has an R square as large as 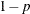 when predicted from the variables listed before it in the statement, the variable is assigned a standardized coefficient
of 0. By default, SINGULAR=1E–8.
when predicted from the variables listed before it in the statement, the variable is assigned a standardized coefficient
of 0. By default, SINGULAR=1E–8.
-
STANDARD
STD
-
standardizes the principal component scores in the OUT= data set to unit variance. If you omit the STANDARD option, the scores
have a variance equal to the corresponding eigenvalue. Note that the STANDARD option has no effect on the eigenvalues themselves.
-
VARDEF=DF | N | WDF | WEIGHT | WGT
-
specifies the divisor to be used in calculating variances and standard deviations. By default, VARDEF=DF. The following table
displays the values and associated divisors:
Table 13.2: continued
|
Value
|
Divisor
|
Formula
|
|
|
DF
|
Error degrees of freedom
|
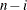
|
(before partialing)
|
| |
|
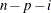
|
(after partialing)
|
|
N
|
Number of observations
|
n
|
|
|
WEIGHT | WGT
|
Sum of weights
|
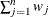
|
|
|
WDF
|
Sum of weights minus one
|
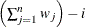
|
(before partialing)
|
| |
|
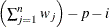
|
(after partialing)
|
In the formulas for VARDEF=DF and VARDEF=WDF, p is the number of degrees of freedom of the variables in the PARTIAL statement, and i is 0 if the NOINT option is specified and 1 otherwise.