The HPPRINCOMP Procedure

ITERGS

The iterative method based on Gram-Schmidt orthogonalization (ITERGS) of Andrecut (2009) overcomes the issue of loss of orthogonality in the NIPALS method by applying Gram-Schmidt reorthogonalization correction to both the loadings and the scores at each iteration step:

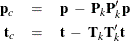
\begin{eqnarray*} \mb{p}_ c & = & \mb{p} ~ -~ \mb{P}_ k\mb{P}_ k’\mb{p} \\ \mb{t}_ c & = & \mb{t} ~ -~ \mb{T}_ k\mb{T}_ k’\mb{t} \end{eqnarray*}

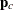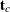Here, $\mb{p}_ c$ and $\mb{t}_ c$ are the corrected loading vector and score vector, respectively. 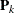$\mb{P}_ k$ is the matrix that is formed by using the first k loadings. 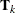$\mb{T}_ k$ is the matrix that is formed by using the first k scores.

The ITERGS method stabilizes the iterative process at the cost of increased computational effort.