The HPFMM Procedure
Latent Variables via Data Augmentation
In order to fit finite Bayesian mixture models, the HPFMM procedure treats the mixture model as a missing data problem and
introduces an assignment variable 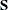 as in Dempster, Laird, and Rubin (1977). Since
as in Dempster, Laird, and Rubin (1977). Since 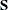 is not observable, it is frequently referred to as a latent variable. The unobservable variable
is not observable, it is frequently referred to as a latent variable. The unobservable variable 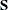 assigns an observation to a component in the mixture model. The number of states, k, might be unknown, but it is known to be finite. Conditioning on the latent variable
assigns an observation to a component in the mixture model. The number of states, k, might be unknown, but it is known to be finite. Conditioning on the latent variable 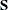 , the component memberships of each observation is assumed to be known, and Bayesian estimation is straightforward for each
component in the finite mixture model. That is, conditional on
, the component memberships of each observation is assumed to be known, and Bayesian estimation is straightforward for each
component in the finite mixture model. That is, conditional on 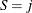 , the distribution of the response is now assumed to be
, the distribution of the response is now assumed to be 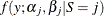 . In other words, each distinct state of the random variable
. In other words, each distinct state of the random variable 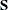 leads to a distinct set of parameters. The parameters in each component individually are then updated using a conjugate Gibbs
sampler (where available) or a Metropolis-Hastings sampling algorithm.
leads to a distinct set of parameters. The parameters in each component individually are then updated using a conjugate Gibbs
sampler (where available) or a Metropolis-Hastings sampling algorithm.
The HPFMM procedure assumes that the random variable 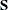 has a discrete multinomial distribution with probability
has a discrete multinomial distribution with probability 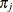 of belonging to a component j; it can occupy one of k states. The distribution for the latent variable
of belonging to a component j; it can occupy one of k states. The distribution for the latent variable 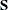 is
is
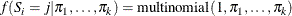
where 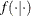 denotes a conditional probability density. The parameters in the density
denotes a conditional probability density. The parameters in the density 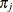 denote the probability that S takes on state j.
denote the probability that S takes on state j.
The HPFMM procedure assumes a conjugate Dirichlet prior distribution on the mixture proportions 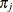 written as:
written as:
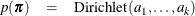
where 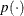 indicates a prior distribution.
indicates a prior distribution.
Using Bayes’ theorem, the likelihood function and prior distributions determine a conditionally conjugate posterior distribution
of 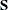 and
and  from the multinomial distribution and Dirichlet distribution, respectively.
from the multinomial distribution and Dirichlet distribution, respectively.
