The HPFMM Procedure
The Form of the Finite Mixture Model
Suppose that you observe realizations of a random variable Y, the distribution of which depends on an unobservable random variable S that has a discrete distribution. S can occupy one of k states, the number of which might be unknown but is at least known to be finite. Since S is not observable, it is frequently referred to as a latent variable.
Let 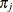 denote the probability that S takes on state j. Conditional on
denote the probability that S takes on state j. Conditional on 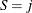 , the distribution of the response Y is assumed to be
, the distribution of the response Y is assumed to be 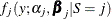 . In other words, each distinct state j of the random variable S leads to a particular distributional form
. In other words, each distinct state j of the random variable S leads to a particular distributional form 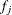 and set of parameters
and set of parameters 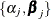 for Y.
for Y.
Let 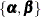 denote the collection of
denote the collection of 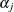 and
and 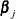 parameters across all j = 1 to k. The marginal distribution of Y is obtained by summing the joint distribution of Y and S over the states in the support of S:
parameters across all j = 1 to k. The marginal distribution of Y is obtained by summing the joint distribution of Y and S over the states in the support of S:
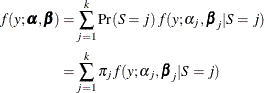
This is a mixture of distributions, and the 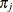 are called the mixture (or prior) probabilities. Because the number of states k of the latent variable S is finite, the entire model is termed a finite mixture (of distributions) model.
are called the mixture (or prior) probabilities. Because the number of states k of the latent variable S is finite, the entire model is termed a finite mixture (of distributions) model.
The finite mixture model can be expressed in a more general form by representing  and
and 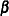 in terms of regressor variables and parameters with optional additional scale parameters for
in terms of regressor variables and parameters with optional additional scale parameters for 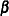 . The section Notation for the Finite Mixture Model develops this in detail.
. The section Notation for the Finite Mixture Model develops this in detail.
