The HPSPLIT Procedure

Pruning

You can choose to prune by the following pattern, which uses the by-metric to choose a node to prune back to a leaf at each iteration until the per-leaf change in the until-metric is operator value times the per-leaf change in the until-metric of replacing the full tree with a single leaf:

PRUNE by-metric / until-metric operator value;

For example, the following statement prunes by average square error until the number of leaves falls below (or is equal to) 3:

PRUNE ASE / N <= 3;

The inequality is necessary because PROC HPSPLIT prunes by removing entire nodes and replacing them with leaves.

The by-metric is used to choose which node to replace with a leaf during each pruning step. The smallest global increase (or largest decrease) in the specified metric is the criterion that is used to choose the node to replace. After the pruner chooses the leaf, it uses the until-metric to determine whether to terminate pruning.

For example, consider the following statement:

PRUNE GINI / ENTROPY >= 1.0;

This statement chooses the node that has the least global change (smallest increase or largest decrease) in the Gini statistic when the node is made into a leaf. It also instructs PROC HPSPLIT to terminate when removing the node causes a change in global entropy per leaf that is greater than or equal to the per-leaf change in entropy that is caused by replacing the original tree by a single leaf.

To be more precise, if the original tree has an entropy of $E_0$ and has $N_0$ leaves, and if trimming away the whole tree to a stump results in a tree that has an entropy of $E_ s$ (and, because it is a stump, just one leaf), then the per-leaf change in entropy is

$\begin{equation*} \left. \frac{\Delta E}{\Delta N} \right|_0 = \frac{E_0 - E_ s}{N_0 - 1} \end{equation*}$

If the node, n, that is chosen by the pruner has an entropy of $E_ n$ , $N_ n$ leaves, and an entropy of $E_\lambda$ if it were replaced by a leaf, then

$\begin{equation*} \left. \frac{\Delta E}{\Delta N} \right|_ n = \frac{E_ n - E_\lambda }{N_ n - 1} \end{equation*}$

The preceding statement would cause the pruner to terminate when

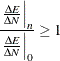
$\begin{equation*} \frac{\left. \frac{\Delta E}{\Delta N} \right|_ n}{\left. \frac{\Delta E}{\Delta N} \right|_0} \ge 1 \end{equation*}$

If the original tree’s until-metric is less than the full tree’s until-metric, as can be true for a significantly overfitted tree that has a validation set, the denominator in the preceding equation is set to 0 (and the equation is suitably transformed). Setting the denominator to 0 selects the subtree that immediately precedes the first increase (or no change) in until-metric.

For all until-metrics except N, the default operator is >= and the default value is 1.0. For the N until-metric, the default operator is <= and the default value is 5.