-
CLB
-
requests the 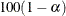 % upper and lower confidence limits for the parameter estimates. By default, the 95% limits are computed; you can use the
ALPHA=
option in the PROC HPQUANTSELECT
statement to change the
% upper and lower confidence limits for the parameter estimates. By default, the 95% limits are computed; you can use the
ALPHA=
option in the PROC HPQUANTSELECT
statement to change the  level.
level.
-
INCLUDE=n
INCLUDE=single-effect
INCLUDE=(effects)
-
forces effects to be included in all models. If you specify INCLUDE=n, then the first n effects that are listed in the MODEL
statement are included in all models. If you specify INCLUDE=single-effect or if you specify a list of effects within parentheses, then the specified effects are forced into all models. The effects
that you specify in the INCLUDE= option must be explanatory effects that are defined in the MODEL
statement.
-
NOINT
-
suppresses the intercept term that is otherwise included in the model.
-
ORDERSELECT
-
specifies that, for the selected model, effects be displayed in the order in which they first entered the model. If you do
not specify this option, then effects in the selected model are displayed in the order in which they appear in the MODEL statement.
-
QUANTILES=number-list
QUANTILE=number-list
-
specifies the quantile levels for the quantile regression. You can specify any number of quantile levels in 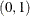 . If you do not specify this option, the HPQUANTSELECT procedure performs median regression effect selection that corresponds
to QUANTILE=0.5.
. If you do not specify this option, the HPQUANTSELECT procedure performs median regression effect selection that corresponds
to QUANTILE=0.5.
-
SPARSITY(<BF | HS> <IID>)
-
specifies the suboptions for estimating the sparsity function. You can specify the Bofinger method by using the BF suboption
or the Hall-Sheather method by using the HS suboption. By default, the Hall-Sheather method is used. You can also specify
the IID suboption to assume that the quantile regression errors satisfy the independently and identically distributed (iid)
assumption. Let 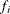 and
and 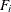 , respectively, denote the probability density function and the cumulative distribution function of the ith error for
, respectively, denote the probability density function and the cumulative distribution function of the ith error for 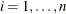 . The iid assumption means that there exist f and
. The iid assumption means that there exist f and 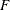 such that
such that 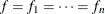 and
and 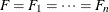 . If you specify the IID option, the covariance matrix of the parameter estimates,
. If you specify the IID option, the covariance matrix of the parameter estimates, 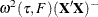 , is adopted for computing the confidence limits and the Wald statistics, where
, is adopted for computing the confidence limits and the Wald statistics, where 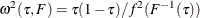 . By default, the covariance matrix of the parameter estimates is non-iid and takes the sandwich form:
. By default, the covariance matrix of the parameter estimates is non-iid and takes the sandwich form: 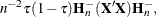 where
where 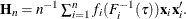 For more information, see the section Details: HPQUANTSELECT Procedure.
For more information, see the section Details: HPQUANTSELECT Procedure.
-
START=n
START=single-effect
START=(effects)
-
begins the effect-selection process in the forward and stepwise selection methods from the initial model that you designate.
If you specify START=n, then the starting model consists of the first n effects listed in the MODEL
statement. If you specify START=single-effect or if you specify a list of effects within parentheses, then the starting model consists of these specified effects. The
effects that you specify in the START= option must be explanatory effects defined in the MODEL
statement. The START= option is not available when you specify METHOD=BACKWARD in the SELECTION
statement.
-
STB
-
produces standardized regression coefficients. A standardized regression coefficient is computed by dividing a parameter estimate
by the ratio of the sample standard deviation of the dependent variable to the sample standard deviation of the regressor.
-
TOL
-
produces tolerance values for the estimates. Tolerance for a parameter is defined as 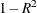 , where
, where 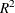 is obtained from the ordinary least squares regression of the parameter on all other parameters in the model.
is obtained from the ordinary least squares regression of the parameter on all other parameters in the model.
-
VIF
-
produces variance inflation factors in the parameter estimates table. Variance inflation is the reciprocal of tolerance.
