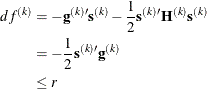-
ABSCONV=r
ABSTOL=r
-
specifies an absolute function convergence criterion. For minimization, the termination criterion is 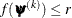 , where
, where 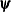 is the vector of parameters in the optimization and
is the vector of parameters in the optimization and 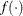 is the objective function. The default value of r is the negative square root of the largest double-precision value, which serves only as a protection against overflows.
is the objective function. The default value of r is the negative square root of the largest double-precision value, which serves only as a protection against overflows.
-
ABSFCONV=r <n>
ABSFTOL=r<n>
-
specifies an absolute function difference convergence criterion. For all techniques except NMSIMP, the termination criterion
is a small change of the function value in successive iterations:
Here, 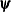 denotes the vector of parameters that participate in the optimization, and
denotes the vector of parameters that participate in the optimization, and 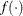 is the objective function. The same formula is used for the NMSIMP technique, but
is the objective function. The same formula is used for the NMSIMP technique, but 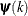 is defined as the vertex with the lowest function value, and
is defined as the vertex with the lowest function value, and 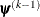 is defined as the vertex with the highest function value in the simplex. The default value is r=0. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
is defined as the vertex with the highest function value in the simplex. The default value is r=0. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
-
ABSGCONV=r <n>
ABSGTOL=r<n>
-
specifies an absolute gradient convergence criterion. The termination criterion is a small maximum absolute gradient element:
Here, 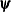 denotes the vector of parameters that participate in the optimization, and
denotes the vector of parameters that participate in the optimization, and 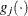 is the gradient of the objective function with respect to the jth parameter. This criterion is not used by the NMSIMP technique. The default value is r=1E–5. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
is the gradient of the objective function with respect to the jth parameter. This criterion is not used by the NMSIMP technique. The default value is r=1E–5. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
-
COMPONENTINFO
COMPINFO
CINFO
-
produces a table with additional details about the fitted model components.
-
COV
-
produces the covariance matrix of the parameter estimates. For maximum likelihood estimation, this matrix is based on the
inverse (projected) Hessian matrix. For Bayesian estimation, it is the empirical covariance matrix of the posterior estimates.
The covariance matrix is shown for all parameters, even if they did not participate in the optimization or sampling.
-
COVI
-
produces the inverse of the covariance matrix of the parameter estimates. For maximum likelihood estimation, the covariance
matrix is based on the inverse (projected) Hessian matrix. For Bayesian estimation, it is the empirical covariance matrix
of the posterior estimates. This matrix is then inverted by sweeping, and rows and columns that correspond to linear dependencies
or singularities are zeroed.
-
CORR
-
produces the correlation matrix of the parameter estimates. For maximum likelihood estimation this matrix is based on the
inverse (projected) Hessian matrix. For Bayesian estimation, it is based on the empirical covariance matrix of the posterior
estimates.
-
CRITERION=keyword
CRIT=keyword
-
specifies the criterion by which the HPFMM procedure ranks models when multiple models are evaluated during maximum likelihood
estimation. You can choose from the following keywords to rank models:
- AIC
-
based on Akaike’s information criterion
- AICC
-
based on the bias-corrected AIC criterion
- BIC
-
based on the Bayesian information criterion
- GRADIENT
-
based on the largest element of the gradient (in absolute value)
- LOGL | LL
-
based on the mixture log likelihood
- PEARSON
-
based on the Pearson statistic
The default is CRITERION=BIC.
-
DATA=SAS-data-set
-
names the SAS data set to be used by PROC HPFMM. The default is the most recently created data set.
-
EXCLUSION=NONE | ANY | ALL
EXCLUDE=NONE | ANY | ALL
-
specifies how the HPFMM procedure handles support violations of observations. For example, in a mixture of two Poisson variables,
negative response values are not possible. However, in a mixture of a Poisson and a normal variable, negative values are possible,
and their likelihood contribution to the Poisson component is zero. An observation that violates the support of one component
distribution of the model might be a valid response with respect to one or more other component distributions. This requires
some nuanced handling of support violations in mixture models.
The default exclusion technique, EXCLUSION=ALL, removes an observation from the analysis only if it violates the support of
all component distributions. The other extreme, EXCLUSION=NONE, permits an observation into the analysis regardless of support
violations. EXCLUSION=ANY removes observations from the analysis if the response violates the support of any component distributions.
In the single-component case, EXCLUSION=ALL and EXCLUSION=ANY are identical.
-
FCONV=r<n>
FTOL=r<n>
-
specifies a relative function convergence criterion that is based on the relative change of the function value. For all techniques
except NMSIMP, PROC HPFMM terminates when there is a small relative change of the function value in successive iterations:
Here, 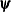 denotes the vector of parameters that participate in the optimization, and
denotes the vector of parameters that participate in the optimization, and 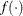 is the objective function. The same formula is used for the NMSIMP technique, but
is the objective function. The same formula is used for the NMSIMP technique, but 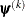 is defined as the vertex with the lowest function value, and
is defined as the vertex with the lowest function value, and 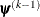 is defined as the vertex with the highest function value in the simplex.
is defined as the vertex with the highest function value in the simplex.
The default is 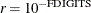 , where FDIGITS is by default
, where FDIGITS is by default 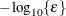 , and
, and  is the machine precision. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process terminates.
is the machine precision. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process terminates.
-
FCONV2=r<n>
FTOL2=r<n>
-
specifies a relative function convergence criterion that is based on the predicted reduction of the objective function. For
all techniques except NMSIMP, the termination criterion is a small predicted reduction
of the objective function. The predicted reduction
is computed by approximating the objective function f by the first two terms of the Taylor series and substituting the Newton step:
For the NMSIMP technique, the termination criterion is a small standard deviation of the function values of the 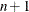 simplex vertices
simplex vertices 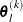 ,
, 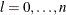 ,
,
where 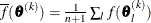 . If there are
. If there are 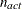 boundary constraints active at
boundary constraints active at 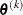 , the mean and standard deviation are computed only for the
, the mean and standard deviation are computed only for the 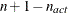 unconstrained vertices.
unconstrained vertices.
The default value is r = 1E–6 for the NMSIMP technique and r = 0 otherwise. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process terminates.
-
FITDETAILS
-
requests that the "Optimization Information," "Iteration History," and "Fit Statistics" tables be produced for all optimizations
when models with different number of components are evaluated. For example, the following statements fit a binomial regression
model with up to three components and produces fit and optimization information for all three:
proc hpfmm fitdetails;
model y/n = x / kmax=3;
run;
Without the FITDETAILS option, only the "Fit Statistics" table for the selected model is displayed.
In Bayesian estimation, the FITDETAILS option displays the following tables for each model that the procedure fits: "Bayes
Information," "Iteration History," "Prior Information," "Fit Statistics," "Posterior Summaries," "Posterior Intervals," and
any requested diagnostics tables. The "Iteration History" table appears only if the BAYES
statement includes the INITIAL=
MLE option.
Without the FITDETAILS option, these tables are listed only for the selected model.
-
GCONV=r<n>
GTOL=r<n>
-
specifies a relative gradient convergence criterion. For all techniques except CONGRA and NMSIMP, the termination criterion
is a small normalized predicted function reduction:
Here, 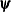 denotes the vector of parameters that participate in the optimization,
denotes the vector of parameters that participate in the optimization, 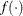 is the objective function, and
is the objective function, and 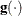 is the gradient. For the CONGRA technique (where a reliable Hessian estimate
is the gradient. For the CONGRA technique (where a reliable Hessian estimate 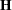 is not available), the following criterion is used:
is not available), the following criterion is used:
This criterion is not used by the NMSIMP technique. The default value is r=1E–8. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process can terminate.
-
HESSIAN
-
displays the Hessian matrix of the model. This option is not available for Bayesian estimation.
-
INVALIDLOGL=r
-
specifies the value assumed by the HPFMM procedure if a log likelihood cannot be computed (for example, because the value
of the response variable falls outside of the response distribution’s support). The default value is –1E20.
-
ITDETAILS
-
adds parameter estimates and gradients to the "Iteration History" table. If the HPFMM procedure centers or scales the model
variables (or both), the parameter estimates and gradients reported during the iteration refer to that scale. You can suppress
centering and scaling with the NOCENTER
option.
-
MAXFUNC=n
MAXFU=n
-
specifies the maximum number of function calls in the optimization process. The default values are as follows, depending on
the optimization technique:
The optimization can terminate only after completing a full iteration. Therefore, the number of function calls that are actually
performed can exceed the number that is specified by the MAXFUNC= option. You can choose the optimization technique with the
TECHNIQUE=
option.
-
MAXITER=n
MAXIT=n
-
specifies the maximum number of iterations in the optimization process. The default values are as follows, depending on the
optimization technique:
These default values also apply when n is specified as a missing value. You can choose the optimization technique with the TECHNIQUE=
option.
-
MAXTIME=r
-
specifies an upper limit of r seconds of CPU time for the optimization process. The time is checked only at the end of each iteration. Therefore, the actual
run time might be longer than the specified time. By default, CPU time is not limited.
-
MINITER=n
MINIT=n
-
specifies the minimum number of iterations. The default value is 0. If you request more iterations than are actually needed
for convergence to a stationary point, the optimization algorithms can behave strangely. For example, the effect of rounding
errors can prevent the algorithm from continuing for the required number of iterations.
-
NAMELEN=number
-
specifies the length to which long effect names are shortened. The default and minimum value is 20.
-
NOCENTER
-
requests that regressor variables not be centered or scaled. By default the HPFMM procedure centers and scales columns of
the 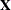 matrix if the models contain intercepts. If NOINT
options in MODEL
statements are in effect, the columns of
matrix if the models contain intercepts. If NOINT
options in MODEL
statements are in effect, the columns of 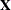 are scaled but not centered. Centering and scaling can help with the stability of estimation and sampling algorithms. The
HPFMM procedure does not produce a table of the centered and scaled coefficients and provides no user control over the type
of centering and scaling that is applied. The NOCENTER option turns any centering and scaling off and processes the raw values
of the continuous variables.
are scaled but not centered. Centering and scaling can help with the stability of estimation and sampling algorithms. The
HPFMM procedure does not produce a table of the centered and scaled coefficients and provides no user control over the type
of centering and scaling that is applied. The NOCENTER option turns any centering and scaling off and processes the raw values
of the continuous variables.
-
NOCLPRINT<=number>
-
suppresses the display of the "Class Level Information" table if you do not specify number. If you specify number, the values of the classification variables are displayed for only those variables whose number of levels is less than number. Specifying a number helps to reduce the size of the "Class Level Information" table if some classification variables have a large number of levels.
-
NOITPRINT
-
suppresses the display of the "Iteration History Information" table.
-
NOPRINT
-
suppresses the normal display of tabular and graphical results. The NOPRINT option is useful when you want to create only
one or more output data sets with the procedure. This option temporarily disables the Output Delivery System (ODS); see Chapter 20: Using the Output Delivery System in SAS/STAT 13.2 User's Guide, for more information.
-
PARMSTYLE=EFFECT | LABEL
-
specifies the display style for parameters and effects. The HPFMM procedure can display parameters in two styles:
-
The EFFECT style (which is used by the MIXED and GLIMMIX procedure, for example) identifies a parameter with an "Effect" column
and adds separate columns for the CLASS
variables in the model.
-
The LABEL style creates one column, named Parameter, that combines the relevant information about a parameter into a single
column. If your model contains multiple CLASS
variables, the LABEL style might use space more economically.
The EFFECT style is the default for models that contain effects; otherwise the LABEL style is used (for example, in homogeneous
mixtures). You can change the display style with the PARMSTYLE= option. Regardless of the display style, ODS output data sets
that contain information about parameter estimates contain columns for both styles.
-
PARTIAL=variable
MEMBERSHIP=variable
-
specifies a variable in the input data set that identifies component membership. You can specify missing values for observations
whose component membership is undetermined; this is known as a partial classification (McLachlan and Peel, 2000, p. 75). For observations with known membership, the likelihood contribution is no longer a mixture. If observation i is known to be a member of component m, then its log likelihood contribution is
Otherwise, if membership is undetermined, it is
The variable specified in the PARTIAL= option can be numeric or character. In case of a character variable, the variable must appear in
the CLASS
statement. If the PARTIAL= variable appears in the CLASS
statement, the membership assignment is made based on the levelized values of the variable, as shown in the "Class Level
Information" table. Invalid values of the PARTIAL= variable are ignored.
In a model in which label switching is a problem, the switching can sometimes be avoided by assigning just a few observations
to categories. For example, in a three-component model, switches might be prevented by assigning the observation with the
smallest response value to the first component and the observation with the largest response value to the last component.
-
PLOTS <(global-plot-options)> <=plot-request <(options)>>
PLOTS <(global-plot-options)> <=(plot-request <(options)> <... plot-request <(options)>>)>
-
controls the plots produced through ODS Graphics.
ODS Graphics must be enabled before plots can be requested. For example:
ods graphics on;
proc hpfmm data=yeast seed=12345;
model count/n = / k=2;
freq f;
performance nthreads=2;
bayes;
run;
ods graphics off;
Global Plot Options
The global-plot-options apply to all relevant plots generated by the HPFMM procedure. The global-plot-options supported by the HPFMM procedure are as follows:
-
UNPACKPANEL
UNPACK
-
displays each graph separately. (By default, some graphs can appear together in a single panel.)
-
ONLY
-
produces only the specified plots. This option is useful if you do not want the procedure to generate all default graphics,
but only the ones specified.
Specific Plot Options
The following listing describes the specific plots and their options.
-
ALL
-
requests that all plots appropriate for the analysis be produced.
-
NONE
-
requests that no ODS graphics be produced.
-
DENSITY <(density-options)>
-
requests a plot of the data histogram and mixture density function. This graphic is a default graphic in models without effects
in the MODEL
statements and is available only in these models. Furthermore, all distributions involved in the mixture must be continuous.
You can specify the following density-options to modify the plot:
-
CUMULATIVE
CDF
-
displays the histogram and densities in cumulative form.
-
NBINS=n
BINS=n
-
specifies the number of bins in the histogram; n is greater than or equal to 0. By default, the HPFMM procedure computes a suitable bin width and number of bins, based on
the range of the response and the number of usable observations. The option has no effect for binary data.
-
NOCOMPONENTS
NOCOMP
-
suppresses the component densities from the plot. If the component densities are displayed, they are scaled so that their
sum equals the mixture density at any point on the graph. In single-component models, this option has no effect.
-
NODENSITY
NODENS
-
suppresses the computation of the mixture density (and the component densities if the COMPONENTS suboption is specified).
If you specify the NOHISTOGRAM and the NODENSITY option, no graphic is produced.
-
NOLABEL
-
suppresses the component identification with labels. By default, the HPFMM procedure labels component densities in the legend
of the plot. If you do not specify a model label with the LABEL=
option in the MODEL
statement, an identifying label is constructed from the parameter estimates that are associated with the component. In this
case the parameter values are not necessarily the mean and variance of the distribution; the values used to identify the densities
on the plot are chosen to simplify linking between graphical and tabular results.
-
NOHISTOGRAM
NOHIST
-
suppresses the computation of the histogram of the raw values. If you specify the NOHISTOGRAM and the NODENSITY option, no
graphic is produced.
-
NPOINTS=n
N=n
-
specifies the number of values used to compute the density functions; n is greater than or equal to 0. The default is N=200.
-
WIDTH=value
BINWIDTH=value
-
specifies the bin width for the histogram. The value is specified in units of the response variable and must be positive. The option has no effect for binary data.
-
TRACE <(tadpanel-options)>
-
requests a trace panel with posterior diagnostics for a Bayesian analysis. If a BAYES
statement is present, the trace panel plots are generated by default, one for each sampled parameter. You can specify the
following tadpanel-options to modify the graphic:
-
BOX
BOXPLOT
-
replaces the autocorrelation plot with a box plot of the posterior sample.
-
SMOOTH=NONE | MEAN | SPLINE
-
adds a reference estimate to the trace plot. By default, SMOOTH=NONE. SMOOTH=MEAN uses the arithmetic mean of the trace as
the reference. SMOOTH=SPLINE adds a penalized B-spline.
-
REFERENCE= reference-style
-
adds vertical reference lines to the density plot, trace plot, and box plot. The available options for the reference-style are:
- NONE
-
suppresses the reference lines
- EQT
-
requests equal-tail intervals
- HPD
-
requests intervals of highest posterior density. The level for the credible or HPD intervals is chosen based on the "Posterior
Interval Statistics" table.
- PERCENTILES
-
(or PERC) for percentiles. Up to three percentiles can be displayed, as based on the "Posterior Summary Statistics" table.
The default is REFERENCE=EQT.
-
UNPACK
-
unpacks the panel graphic and displays its elements as separate plots.
-
CRITERIONPANEL <(critpanel-options)>
-
requests a plot for comparing the model fit criteria for different numbers of components. This plot is available only if you
also specify the KMAX
option in at least one MODEL
statement. The plot includes different criteria, depending on whether you are using maximum likelihood or Bayesian estimation.
You can specify the following critpanel-option to modify the plot:
-
UNPACK
-
unpacks the panel plot and displays its elements as separate plots, one for each fit criterion.
-
SEED=n
-
determines the random number seed for analyses that depend on a random number stream. If you do not specify a seed or if you
specify a value less than or equal to zero, the seed is generated from reading the time of day from the computer clock. The
largest possible value for the seed is 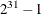 . The seed value is reported in the "Model Information" table.
. The seed value is reported in the "Model Information" table.
You can use the SYSRANDOM and SYSRANEND macro variables after a PROC HPFMM run to query the initial and final seed values.
However, using the final seed value as the starting seed for a subsequent analysis does not continue the random number stream
where the previous analysis left off. The SYSRANEND macro variable provides a mechanism to pass on seed values to ensure that
the sequence of random numbers is the same every time you run an entire program.
Analyses that use the same (nonzero) seed are not completely reproducible if they are executed with a different number of
threads since the random number streams in separate threads are independent. You can control the number of threads used by
the HPFMM procedure with system options or through the PERFORMANCE
statement in the HPFMM procedure.
-
SINGCHOL=number
-
tunes the singularity criterion in Cholesky decompositions. The default is 1E4 times the machine epsilon; this product is
approximately 1E–12 on most computers.
-
SINGRES=number
-
sets the tolerance for which the residual variance or scale parameter is considered to be zero. The default is 1E4 times the
machine epsilon; this product is approximately 1E–12 on most computers.
-
SINGULAR=number
-
tunes the general singularity criterion applied by the HPFMM procedure in sweeps and inversions. The default is 1E4 times
the machine epsilon; this product is approximately 1E–12 on most computers.
-
TECHNIQUE=keyword
TECH=keyword
-
specifies the optimization technique to obtain maximum likelihood estimates. You can choose from the following techniques
by specifying the appropriate keyword:
- CONGRA
-
performs a conjugate-gradient optimization.
- DBLDOG
-
performs a version of double-dogleg optimization.
- NEWRAP
-
performs a Newton-Raphson optimization combining a line-search algorithm with ridging.
- NMSIMP
-
performs a Nelder-Mead simplex optimization.
- NONE
-
performs no optimization.
- NRRIDG
-
performs a Newton-Raphson optimization with ridging.
- QUANEW
-
performs a dual quasi-Newton optimization.
- TRUREG
-
performs a trust-region optimization.
The default is TECH=QUANEW.
For more details about these optimization methods, see the section Choosing an Optimization Algorithm.
-
ZEROPROB=number
-
tunes the threshold (a value between 0 and 1) below which the HPFMM procedure considers a component mixing probability to
be zero. This affects the calculation of the number of effective components. The default is the square root of the machine
epsilon; this is approximately 1E–8 on most computers.