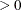Built-In Log-Likelihood Functions :: SAS/STAT(R) 12.3 User's Guide: High-Performance Procedures

Built-In Log-Likelihood Functions

For models in which the distribution of model errors is specified, the HPNLMOD procedure estimates parameters by maximizing the value of a log-likelihood function for the specified distribution. The log-likelihood functions used by PROC HPNLMOD for the supported error distributions are as follows:

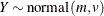
$Y \sim \mr {normal}(m,v)$

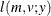
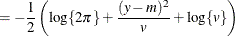
$\displaystyle l(m,v;y)$	$\displaystyle = -\frac12 \left( \log \{ 2\pi \} + \frac{(y-m)^2}{v} + \log \{ v\} \right)$
$\displaystyle \mr {E}[Y]$	$\displaystyle = m$
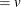
$\displaystyle \mr {Var}[Y]$	$\displaystyle = v$
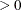
$\displaystyle v$	$\displaystyle > 0$

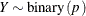
$Y \sim \mr {binary}(p)$

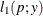
$\displaystyle l_1(p;y)$	$\displaystyle = \left\{ \begin{array}{ll} y \, \, \log \{ p\} & y > 0 \cr 0 \phantom{(1-y)\, \, \log \{ 1-p\} } & \mr {otherwise} \end{array} \right.$
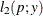
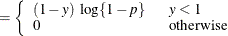
$\displaystyle l_2(p;y)$	$\displaystyle = \left\{ \begin{array}{ll} (1-y)\, \, \log \{ 1-p\} \phantom{0} & y < 1 \cr 0 & \mr {otherwise} \end{array} \right.$
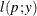
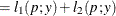
$\displaystyle l(p;y)$	$\displaystyle = l_1(p;y) + l_2(p;y)$
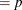
$\displaystyle \mr {E}[Y]$	$\displaystyle = p$
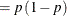
$\displaystyle \mr {Var}[Y]$	$\displaystyle = p\, (1-p)$
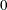
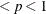
$\displaystyle 0$	$\displaystyle < p < 1$

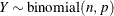
$Y \sim \mr {binomial}(n,p)$

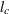
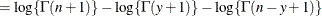
$\displaystyle l_ c$	$\displaystyle = \log \{ \Gamma (n+1)\} - \log \{ \Gamma (y+1)\} - \log \{ \Gamma (n-y+1)\}$
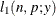
$\displaystyle l_1(n,p;y)$	$\displaystyle = \left\{ \begin{array}{ll} y \, \, \log \{ p\} & y > 0 \cr 0 \phantom{(n-y)\, \, \log \{ 1-p\} } & \mr {otherwise} \end{array} \right.$
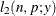
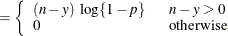
$\displaystyle l_2(n,p;y)$	$\displaystyle = \left\{ \begin{array}{ll} (n-y)\, \, \log \{ 1-p\} \phantom{0} & n-y > 0 \cr 0 & \mr {otherwise} \end{array} \right.$
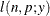
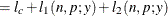
$\displaystyle l(n,p;y)$	$\displaystyle = l_ c + l_1(n,p;y) + l_2(n,p;y)$
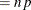
$\displaystyle \mr {E}[Y]$	$\displaystyle = n\, p$
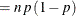
$\displaystyle \mr {Var}[Y]$	$\displaystyle = n\, p\, (1-p)$
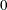
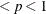
$\displaystyle 0$	$\displaystyle < p < 1$

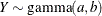
$Y \sim \mr {gamma}(a,b)$

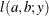
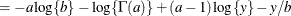
$\displaystyle l(a,b;y)$	$\displaystyle = -a\log \{ b\} - \log \{ \Gamma (a)\} + (a-1)\log \{ y\} - y/b$
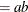
$\displaystyle \mr {E}[Y]$	$\displaystyle = ab$
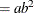
$\displaystyle \mr {Var}[Y]$	$\displaystyle = ab^2$
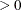
$\displaystyle a$	$\displaystyle > 0$
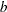
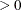
$\displaystyle b$	$\displaystyle > 0$

This parameterization of the gamma distribution differs from the parameterization that the GLIMMIX and GENMOD procedures use. The scale parameter in PROC HPNLMOD is expressed as the inverse of the scale parameter that PROC GLIMMIX and PROC GENMOD use. The PROC HPNLMOD parameter represents the scale of the magnitude of the residuals. The scale parameter in PROC GLIMMIX can be estimated by using the following statements:

proc glimmix;
   model y = x / dist=gamma s;
run;

The following statements show how to use PROC HPNLMOD to estimate the equivalent scale parameter:

proc hpnlmod;
   parms b0=1 b1=0 scale=14;
   linp = b0 + b1*x;
   mu   = exp(linp);
   b    = mu*scale;
   model y ~ gamma(1/scale,b);
run;

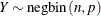
$Y \sim \mr {negbin}(n,p)$

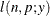
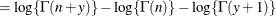
$\displaystyle l(n,p;y)$	$\displaystyle = \log \{ \Gamma (n+y)\} - \log \{ \Gamma (n)\} - \log \{ \Gamma (y+1)\}$
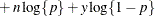
$\displaystyle$	$\displaystyle \mbox{ } +n \log \{ p\} + y \log \{ 1-p\}$
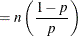
$\displaystyle \mr {E}[Y]$	$\displaystyle = n\left(\frac{1-p}{p}\right)$
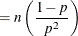
$\displaystyle \mr {Var}[Y]$	$\displaystyle = n\left(\frac{1-p}{p^2}\right)$
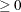
$\displaystyle n$	$\displaystyle \ge 0$
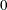
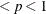
$\displaystyle 0$	$\displaystyle < p < 1$

The parameter can be real-numbered; it does not have to be integer-valued.

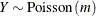
$Y \sim \mr {Poisson}(m)$

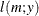
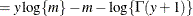
$\displaystyle l(m;y)$	$\displaystyle = y \log \{ m\} - m - \log \{ \Gamma (y + 1)\}$
$\displaystyle \mr {E}[Y]$	$\displaystyle = m$
$\displaystyle \mr {Var}[Y]$	$\displaystyle = m$
$\displaystyle m$	$\displaystyle > 0$

The HPNLMOD Procedure

Built-In Log-Likelihood Functions