Fit Analyses

Nonparametric Smoothers

For a simple regression model with one or two explanatory variables,

$y_{i} = f( x_{i}) + \varepsilon_{i}$

a smoother $\hat{f_\lambda}(x)$ is a function that summarizes the trend of Y as a function of X. It can enhance the visual perception of either a Y-by-X scatter plot or a rotating plot. The smoothing parameter $\lambda$ controls the smoothness of the estimate.

With one explanatory variable in the model, $\hat{f_\lambda}(x)$ is called a scatter plot smoother. SAS/INSIGHT software provides nonparametric curve estimates from smoothing spline, kernel, loess (nearest neighbors local polynomial), and fixed bandwidth local polynomial smoothers.

For smoothing spline, kernel, and fixed bandwidth local polynomial smoothers, SAS/INSIGHT software derives the smoothing parameter $\lambda$ from a constant c that is independent of the units of X. For a loess smoother, the smoothing parameter $\lambda$ is a positive constant $\alpha$ .

With two explanatory variables in the model, $\hat{f_\lambda}(x)$ is called a surface smoother. SAS/INSIGHT software provides nonparametric surface estimates from thin-plate smoothing spline and kernel smoothers. The explanatory variables are scaled by their corresponding sample interquartile ranges. The smoothing parameter $\lambda$ is derived from a constant c and both are independent of the units of X.

Similar to parametric regression, the R² value for an estimate is calculated as

$R^2 = 1 - \frac{\sum_{i=1}^n{( y_{i}- \hat{f_\lambda}( x_{i}) )^2}}{\sum_{i=1}^n{( y_{i}-{{\overline y}})^2} }$

You can use the following methods to choose the $\lambda$ value:

DF: uses the 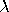$\lambda$ value that makes the resulting smoothing estimate have the specified degrees of freedom (df).
GCV: uses the 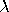$\lambda$ value that minimizes the generalized cross validation (GCV) mean squared error.
C Value: uses the 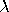$\lambda$ value derived from the specified c value for nonparametric smoothers other than the loess smoother.
Alpha: uses the specified 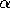$\alpha$ value for the loess estimator.

If you specify a DF value for a smoother, an iterative procedure is used to find the estimate with the specified df. You can choose a convergence criterion ${\gamma}$ based on either the relative difference or the absolute difference. A smoother satisfying the following conditions is then created:

$\frac{| df(\rm{fitted})-df(\rm{specified})|}{df(\rm{specified})} \lt \gamma {for relative difference}$

$| df(\rm{fitted})-df(\rm{specified})| \lt \gamma {for absolute difference}$

Smoother Degrees of Freedom

Smoother Generalized Cross Validation

Top of Page