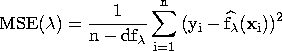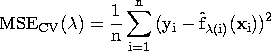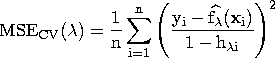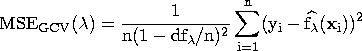Smoother Generalized Cross Validation

Fit Analyses

Smoother Generalized Cross Validation

With the degrees of freedom of an estimate ${ df_{\lambda}}$ ,the mean squared error is given as

$\rm{MSE}(\lambda) = \frac{1}{n- df_{\lambda}} \sum_{i=1}^n{( y_{i}- \hat{f_\lambda}( x_{i}) )^2}$

Cross-validation (CV) estimates the response at each x_i from the smoother that uses only the remaining n-1 observations. The resulting cross validation mean squared error is

$\rm{MSE}_{CV}(\lambda) = \frac{1}n \sum_{i=1}^n{( y_{i}- \hat{f}_{\lambda (i)} ( x_{i}))^2 }$

where ${ \hat{f}_{\lambda(i)}( x_{i}) }$ is the fitted value at x_i computed without the ith observation.

The cross validation mean squared error can also be written as

$\rm{MSE}_{CV}(\lambda) = \frac{1}n \sum_{i=1}^n ( \frac{ y_{i}- \hat{f_\lambda}( x_{i})} {1- h_{\lambda i} } )^2$

where ${ h_{\lambda i}}$ is the ith diagonal element of the $H_{\lambda}$ matrix (Hastie and Tibshirani 1990).

Generalized cross validation replaces ${ h_{\lambda i}}$ by its average value, ${\frac{1}n df_{\lambda}}$ .The generalized cross validation mean squared error is

$\rm{MSE}_{GCV}(\lambda) = \frac{1}{n (1- df_{\lambda}/n)^2 } \sum_{i=1}^n ( y_{i}- \hat{f_\lambda}( x_{i}))^2$

Note	The function ${ \rm{MSE}_{GCV}(\lambda)}$ may have multiple minima, so the value estimated by SAS/INSIGHT software may be only a local minimum, not the global minimum.

Top of Page