Parametric Density

Distribution Analyses

Parametric Density

Parametric density estimation assumes that the data are from a known family of distributions, such as the normal, lognormal, exponential, and Weibull. After choosing Curves:Parametric Density from the menu, you specify the family of distributions in the Parametric Density Estimation dialog, as shown in Figure 38.23.

Figure 38.23: Parametric Density Dialog

The default uses a normal distribution with the sample mean and standard deviation as estimates for $\mu$ and $\sigma$ .You can also specify your own $\mu$ and $\sigma$ parameters for the normal distribution by choosing Method:Specification in the dialog.

For the lognormal, exponential, and Weibull distributions, you can specify your own threshold parameter $\theta$ in the Parameter:MLE, Theta entry field and have the remaining parameters estimated by the maximum-likelihood estimates (MLE) by choosing Method:Sample Estimates/MLE. Otherwise, you can specify all the parameters in the Specification fields and choose Method:Specification in the dialog.

If you select a Weight variable, only normal density can be created. For Method:Sample Estimates/MLE, ${{\overline y_{w}}}$ and s_w are used to display the density with vardef=WDF/WGT; ${{\overline y_{w}}}$ and s_a are used with vardef=DF/N. For Method:Specification, the values in the entry fields Mean/Theta and Sigma are used to display the density with vardef=WDF/WGT; the values of Mean/Theta and Sigma/ ${\sqrt{{\overline w}}}$ are used with vardef=DF/N.

Figure 38.24 displays a normal density estimate with $\mu = 58.4333$ (the sample mean) and $\sigma = 8.2807$ (the sample standard deviation). It also displays a lognormal density estimate with $\theta = 30$ and with $\sigma$ and $\zeta$ estimated by the MLE.

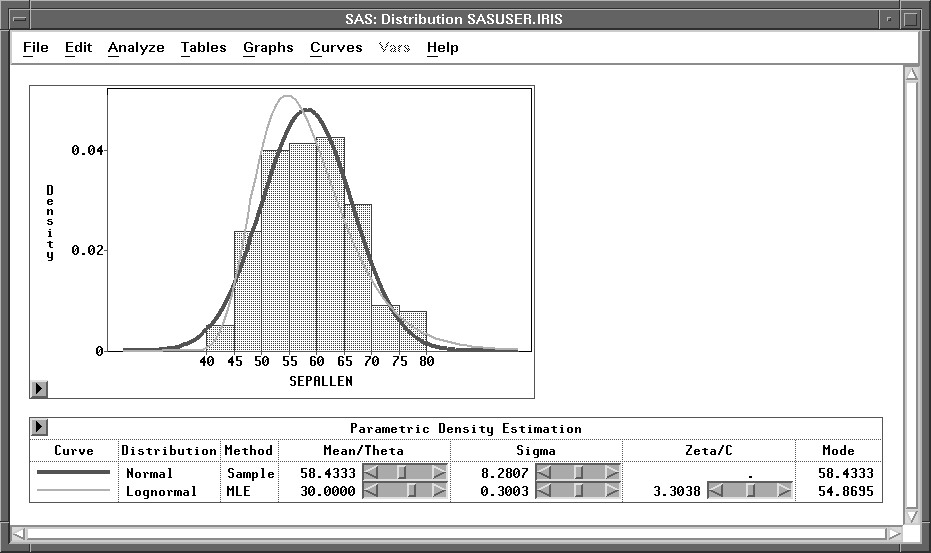
Figure 38.24: Parametric Density Estimation

The Mode is the point with the largest estimated density. Use sliders in the table to change the density estimate. When MLE is used for the lognormal, exponential, and Weibull distributions, changing the value of $\theta$ in the Mean/Theta slider also causes the remaining parameters to be estimated by the MLE for the new $\theta$ .

Top of Page