The SHEWHART Procedure
Nonnormal Process Data
Note: See Nonnormal Process Data in the SAS/QC Sample Library.
A number of authors have pointed out that Shewhart charts for subgroup means work well whether the measurements are normally distributed or not.[55] On the other hand, the interpretation of standard control charts for individual measurements (X charts) is affected by departures from normality.
In situations involving a large number of measurements, it might be possible to subgroup the data and construct an 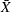 chart instead of an X chart. However, the measurements should not be subgrouped arbitrarily for this purpose.[56] If subgrouping is not possible, two alternatives are to transform the data to normality (preferably with a simple transformation
such as the log transformation) or modify the usual limits based on a suitable model for the data distribution.
chart instead of an X chart. However, the measurements should not be subgrouped arbitrarily for this purpose.[56] If subgrouping is not possible, two alternatives are to transform the data to normality (preferably with a simple transformation
such as the log transformation) or modify the usual limits based on a suitable model for the data distribution.
The second of these alternatives is illustrated here with data from a study conducted by a service center. The time taken
by staff members to answer the phone was measured, and the delays were saved as values of a variable named Time in a SAS data set named Calls. A partial listing of Calls is shown in Figure 18.216.
Figure 18.216: Answering Times from the Data Set Calls
| Recnum | Time |
|---|---|
| 1 | 3.233 |
| 2 | 3.110 |
| 3 | 3.136 |
| 4 | 2.899 |
| 5 | 2.838 |
| 6 | 2.459 |
| 7 | 3.716 |
| 8 | 2.740 |
| 9 | 2.487 |
| 10 | 2.635 |
| 11 | 2.676 |
| 12 | 2.905 |
| 13 | 3.431 |
| 14 | 2.663 |
| 15 | 3.437 |
| 16 | 2.823 |
| 17 | 2.596 |
| 18 | 2.633 |
| 19 | 3.235 |
| 20 | 2.701 |
| 21 | 3.202 |
| 22 | 2.725 |
| 23 | 3.151 |
| 24 | 2.464 |
| 25 | 2.662 |
| 26 | 3.188 |
| 27 | 2.640 |
| 28 | 2.541 |
| 29 | 3.033 |
| 30 | 2.993 |
| 31 | 2.636 |
| 32 | 2.481 |
| 33 | 3.191 |
| 34 | 2.662 |
| 35 | 2.967 |
| 36 | 3.300 |
| 37 | 2.530 |
| 38 | 2.777 |
| 39 | 3.353 |
| 40 | 3.614 |
| 41 | 4.288 |
| 42 | 2.442 |
| 43 | 2.552 |
| 44 | 2.613 |
| 45 | 2.731 |
| 46 | 2.780 |
| 47 | 3.588 |
| 48 | 2.612 |
| 49 | 2.579 |
| 50 | 2.871 |