The SHEWHART Procedure

Calculating Probability Limits

The OUTLIMITS= option saves the control limits from the chart in Figure 18.217 in a SAS data set named delaylim, which is listed in Figure 18.218.

Figure 18.218: Control Limits for Standard Chart from the Data Set Calls

_VAR_	_SUBGRP_	_TYPE_	_LIMITN_	_ALPHA_	_SIGMAS_	_LCLI_	_MEAN_	_UCLI_	_STDDEV_
Time	Recnum	ESTIMATE	2	.002699796	3	1.77008	2.91038	4.05068	0.38010

The control limits can be replaced with the corresponding percentiles from a fitted lognormal distribution. The equation for the lognormal density function is

$\begin{array}{ll} f(x) = \frac{1}{x \sqrt {2\pi } \sigma } \exp \left( - \frac{(\log (x) - \zeta )^2}{2 \sigma ^2} \right) & x > 0 \end{array}$

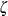where $\sigma$ denotes the shape parameter and $\zeta$ denotes the scale parameter.

The following statements use the CAPABILITY procedure to fit a lognormal model and superimpose the fitted density on a histogram of the data, shown in Figure 18.219:

title 'Lognormal Fit for Delay Distribution';
proc capability data=Calls noprint;
   histogram Time /
      lognormal(threshold=2.3 w=2)
      outfit = Lnfit
      nolegend ;
   inset n = 'Number of Calls'
      lognormal( sigma = 'Shape' (4.2)
                 zeta  = 'Scale' (5.2)
                 theta ) / pos    = ne;
   label Time  = 'Answering Delay (minutes)';
run;

Figure 18.219: Distribution of Delays

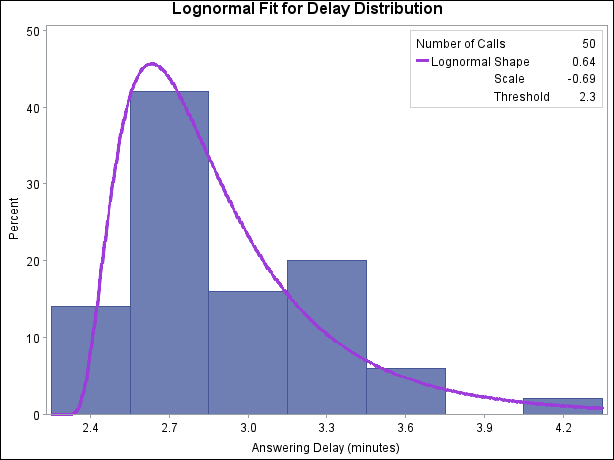
Parameters of the fitted distribution and results of goodness-of-fit tests are saved in the data set Lnfit, which is listed in Figure 18.220. The large p-values for the goodness-of-fit tests are evidence that the lognormal model provides a good fit.

Figure 18.220: Parameters of Fitted Lognormal Model in the Data Set Lnfit

_VAR_	_CURVE_	_LOCATN_	_SCALE_	_SHAPE1_	_MIDPTN_	_ADASQ_	_ADP_	_CVMWSQ_	_CVMP_	_KSD_	_KSP_
Time	LNORMAL	2.3	-0.68910	0.64110	4.2	0.34854	0.47465	0.058737	0.40952	0.092223	0.15

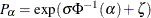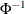The following statements replace the control limits in DELAYLIM with limits computed from percentiles of the fitted lognormal model. The 100 $\alpha$ th percentile of the lognormal distribution is $P_{\alpha } = \exp (\sigma \Phi ^{-1}(\alpha ) + \zeta )$ , where $\Phi ^{-1}$ denotes the inverse standard normal cumulative distribution function. The SHEWHART procedure constructs an X chart with the modified limits, displayed in Figure 18.221.

data delaylim;
   merge delaylim Lnfit;
   drop _sigmas_ ;
   _lcli_ = _locatn_ + exp(_scale_+probit(0.5*_alpha_)*_shape1_);
   _ucli_ = _locatn_ + exp(_scale_+probit(1-.5*_alpha_)*_shape1_);
   _mean_ = _locatn_ + exp(_scale_+0.5*_shape1_*_shape1_);
run;

title 'Lognormal Control Limits for Delays';
proc shewhart data=Calls limits=delaylim;
   irchart Time*Recnum /
      rtmplot   = schematic
      nochart2 ;
   label Recnum = 'Record Number'
         Time   = 'Delay in minutes' ;
run;

Figure 18.221: Adjusted Control Limits for Delays

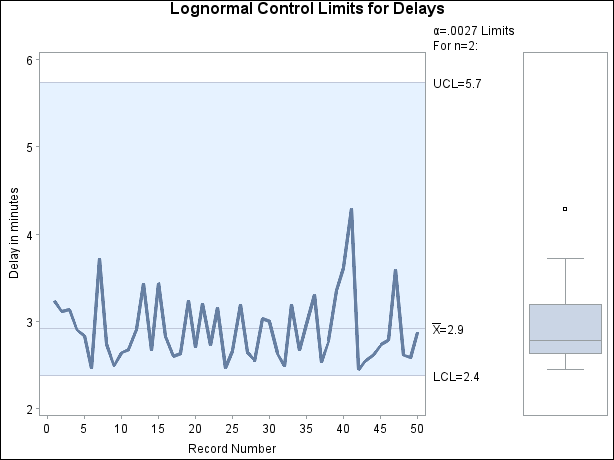
Clearly the process is in control, and the control limits (particularly the lower limit) are appropriate for the data. The particular probability level 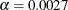$\alpha =0.0027$ associated with these limits is somewhat immaterial, and other values of $\alpha$ such as 0.001 or 0.01 could be specified with the ALPHA= option in the original IRCHART statement.