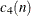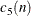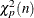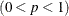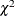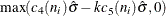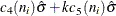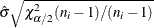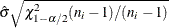SCHART Statement: SHEWHART Procedure
Constructing Charts for Standard Deviations
The following notation is used in this section:
|
|
Process standard deviation (standard deviation of the population of measurements) |
|
|
Standard deviation of measurements in ith subgroup ![\[ s_{i} = \sqrt {(1/(n_ i-1))( (x_{i1} - \bar{X_{i}})^2 + \cdots + (x_{in_{i}} - \bar{X_{i}})^2)} \]](images/qcug_shewhart0226.png) |
|
|
Sample size of ith subgroup |
|
|
Expected value of the standard deviation of n independent normally distributed variables with unit standard deviation |
|
|
Standard error of the standard deviation of n independent observations from a normal population with unit standard deviation |
|
|
100pth percentile |
Plotted Points
Each point on an s chart indicates the value of a subgroup standard deviation ( ). For example, if the tenth subgroup contains the values 12, 15, 19, 16, and 13, the value plotted for this subgroup is
). For example, if the tenth subgroup contains the values 12, 15, 19, 16, and 13, the value plotted for this subgroup is
![\[ s_{10}= \sqrt {((12-15)^2 + (15-15)^2 + (19-15)^2 + (16-15)^2 + (13-15)^2)/4 } = 2.739 \]](images/qcug_shewhart0231.png)
Central Line
By default, the central line for the ith subgroup indicates an estimate for the expected value of  , which is computed as
, which is computed as 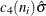 , where
, where 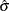 is an estimate of
is an estimate of  . If you specify a known value (
. If you specify a known value (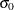 ) for
) for  , the central line indicates the value of
, the central line indicates the value of 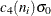 . Note that the central line varies with
. Note that the central line varies with 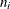 .
.
Control Limits
You can compute the limits in the following ways:
-
as a specified multiple (k) of the standard error of
 above and below the central line. The default limits are computed with k = 3 (these are referred to as
above and below the central line. The default limits are computed with k = 3 (these are referred to as 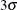 limits).
limits).
-
as probability limits defined in terms of
 , a specified probability that
, a specified probability that  exceeds the limits
exceeds the limits
The following table provides the formulas for the limits:
Table 18.46: Limits for s Charts
|
Control Limits |
|---|
|
LCL = lower limit = |
|
UCL = upper limit = |
|
Probability Limits |
|
LCL = lower limit = |
|
UCL = upper limit = |
The formulas assume that the data are normally distributed. If a standard value 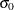 is available for
is available for  , replace
, replace 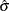 with
with 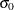 in Table 18.46. Note that the upper and lower limits vary with
in Table 18.46. Note that the upper and lower limits vary with 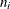 and that the probability limits are asymmetric around the central line.
and that the probability limits are asymmetric around the central line.
You can specify parameters for the limits as follows:
-
Specify k with the SIGMAS= option or with the variable
_SIGMAS_in a LIMITS= data set. -
Specify
 with the ALPHA=
option or with the variable
with the ALPHA=
option or with the variable _ALPHA_in a LIMITS= data set. -
Specify a constant nominal sample size
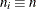 for the control limits with the LIMITN=
option or with the variable
for the control limits with the LIMITN=
option or with the variable _LIMITN_in a LIMITS= data set. -
Specify
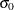 with the SIGMA0=
option or with the variable
with the SIGMA0=
option or with the variable _STDDEV_in a LIMITS= data set.