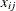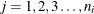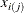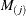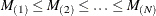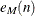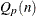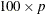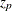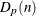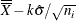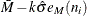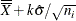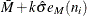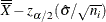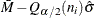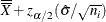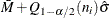BOXCHART Statement: SHEWHART Procedure
- Overview
-
Getting Started

-
Syntax

-
Details

-
Examples
 Using Box Charts to Compare SubgroupsCreating Various Styles of Box-and-Whisker PlotsCreating Notched Box-and-Whisker PlotsCreating Box-and-Whisker Plots with Varying WidthsCreating Box-and-Whisker Plots with Different Line Styles and ColorsComputing the Control Limits for Subgroup MaximumsConstructing Multi-Vari Charts
Using Box Charts to Compare SubgroupsCreating Various Styles of Box-and-Whisker PlotsCreating Notched Box-and-Whisker PlotsCreating Box-and-Whisker Plots with Varying WidthsCreating Box-and-Whisker Plots with Different Line Styles and ColorsComputing the Control Limits for Subgroup MaximumsConstructing Multi-Vari Charts
Constructing Box Charts
The following notation is used in this section:
|
|
Process mean (expected value of the population of measurements) |
|
|
Process standard deviation (standard deviation of the population of measurements) |
|
|
Mean of measurements in ith subgroup |
|
|
Sample size of ith subgroup |
|
N |
The number of subgroups |
|
|
jth measurement in the ith subgroup, |
|
|
jth largest measurement in the ith subgroup: ![\[ x_{i(1)} \leq x_{i(2)} \leq \ldots \leq x_{i(n_{i})} \]](images/qcug_shewhart0016.png) |
|
|
Weighted average of subgroup means |
|
|
Median of the measurements in the ith subgroup: ![\[ M_ i = \left\{ \begin{array}{ll} x_{i((n_ i + 1)/2)} & \mbox{if $n_{i}$ is odd} \\ (x_{i(n_ i/2)} + x_{i((n_ i/2)+1)})/2 & \mbox{if $n_{i}$ is even} \end{array} \right. \]](images/qcug_shewhart0019.png) |
|
|
Average of the subgroup medians: ![\[ \bar{M} = (n_1M_1 + \ldots + n_ NM_ N)/(n_1+\ldots +n_ N) \]](images/qcug_shewhart0021.png) |
|
|
Median of the subgroup medians. Denote the jth largest median by ![\[ \tilde{M} = \left\{ \begin{array}{ll} M_{((N+1)/2)} & \mbox{if } N \mbox{ is odd} \\ (M_{(N/2)} + M_{(N/2)+1})/2 & \mbox{if } N \mbox{ is even} \end{array} \right. \]](images/qcug_shewhart0025.png) |
|
|
Standard error of the median of n independent, normally distributed variables with unit standard deviation (the value of |
|
|
|
|
|
|
|
|
|
Elements of Box-and-Whisker Plots
A box-and-whisker plot is displayed for the measurements in each subgroup on the box chart. Figure 18.14 illustrates the elements of each plot.
Figure 18.14: Box-and-Whisker Plot
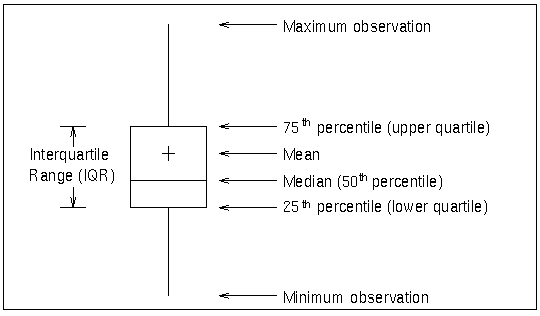
The skeletal style of the box-and-whisker plot shown in Figure 18.14 is the default. You can specify alternative styles with the BOXSTYLE= option; see Example 18.2 or the entry for BOXSTYLE= in Dictionary of Options: SHEWHART Procedure.
Control Limits and Central Line
You can compute the limits in the following ways:
-
as a specified multiple (k) of the standard error of
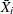 (or
(or 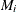 ) above and below the central line. The default limits are computed with k = 3 (these are referred to as
) above and below the central line. The default limits are computed with k = 3 (these are referred to as 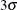 limits).
limits).
-
as probability limits defined in terms of
 , a specified probability that
, a specified probability that 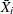 (or
(or 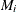 ) exceeds the limits
) exceeds the limits
The CONTROLSTAT= option specifies whether control limits are computed for subgroup means (the default) or subgroup medians. Table 18.6 provides the formulas for the limits.
Table 18.6: Limits and Central Line for Box Charts
|
Control Limits |
|
|---|---|
|
CONTROLSTAT=MEAN |
CONTROLSTAT=MEDIAN |
|
LCLX = lower limit = |
LCLM = lower limit = |
|
Central Line = |
Central Line = |
|
UCLX = upper limit = |
UCLM = upper limit = |
|
Probability Limits |
|
|
CONTROLSTAT=MEAN |
CONTROLSTAT=MEDIAN |
|
LCLX = lower limit = |
LCLM = lower limit = |
|
Central Line = |
Central Line = |
|
UCLX = upper limit = |
UCLM = upper limit = |
In the preceding tables, replace 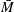 with
with 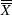 if you specify MEDCENTRAL=
AVGMEAN in addition to CONTROLSTAT=MEDIAN. Likewise, replace
if you specify MEDCENTRAL=
AVGMEAN in addition to CONTROLSTAT=MEDIAN. Likewise, replace 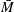 with
with 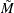 if you specify MEDCENTRAL=MEDMED in addition to CONTROLSTAT=MEDIAN. If standard values
if you specify MEDCENTRAL=MEDMED in addition to CONTROLSTAT=MEDIAN. If standard values 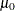 and
and 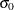 are available for
are available for 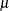 and
and  , replace
, replace 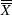 with
with 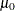 and
and 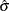 with
with 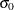 in Table 18.6.
in Table 18.6.
Note that the limits vary with 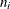 . The formulas for median limits assume that the data are normally distributed.
. The formulas for median limits assume that the data are normally distributed.
You can specify parameters for the limits as follows:
-
Specify k with the SIGMAS= option or with the variable
_SIGMAS_in a LIMITS= data set. -
Specify
 with the ALPHA=
option or with the variable
with the ALPHA=
option or with the variable _ALPHA_in a LIMITS= data set. -
Specify a constant nominal sample size
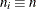 for the control limits with the LIMITN=
option or with the variable
for the control limits with the LIMITN=
option or with the variable _LIMITN_in a LIMITS= data set. -
Specify
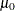 with the MU0=
option or with the variable
with the MU0=
option or with the variable _MEAN_in a LIMITS= data set. -
Specify
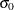 with the SIGMA0=
option or with the variable
with the SIGMA0=
option or with the variable _STDDEV_in a LIMITS= data set.
Note: You can suppress the display of the control limits with the NOLIMITS option. This is useful for creating standard side-by-side box-and-whisker plots.