The MVPMONITOR Procedure

Computing SPE Control Limits

Subsections:

The SPE chart plots the sum of squares of the residuals from the principal component model. If either 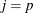$j=p$ or the data matrix has rank less than p, then the SPE statistic is not defined and an SPE chart is not produced. The SPE statistic for observation i is denoted as

\[ Q_{i}=\sum _{k=1}^{p}e_{ik}^{2} \]

where p is the number of variables and 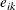$e_{ik}$ is the ith observation for the kth variable in the error matrix, E, in the principal component model

\[ \mb{X} = \mb{TP}^{\prime } + \mb{E} \]

The distribution of 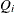$Q_ i$ has been approximated in the literature under different conditions. Two methods of computing control limits for 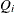$Q_ i$ are implemented by the MVPMONITOR procedure. One method is used when the data that are used to build the principal component model consist of a single measurement per time point. The other method is used when there are multiple measurements per time point (Jensen and Solomon 1972; Nomikos and MacGregor 1995).

One Observation per Time Point

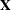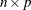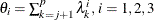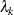When there is a single observation at each time point, the data matrix $\mb{X}$ is $n\times p$, with exactly one observation at each time point in the input data set. The derivation of the control limits uses the central limit theorem approach of Jensen and Solomon (1972). They begin by defining $\theta _ i=\sum _{k=j+1}^ p\lambda _ k^ i,\, i=1,2,3$, where $\lambda _ k$ is the kth eigenvalue from the principal component model.

Then the quantity

\[ z=\frac{\theta _1 \left[ \left( \frac{Q}{\theta _1} \right)^{h_0} -1 - \frac{\theta _2 h_0 \left(h_0 -1 \right)}{\theta _1^2} \right]}{\sqrt {2 \theta _2 h_0^2} } \]

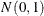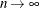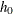is distributed $N\left(0,1 \right)$ as $n \to \infty $, where $h_0$ is defined as 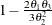$1-\frac{2 \theta _1 \theta _3}{3 \theta _2^2}$. The upper control limit for all 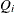$Q_ i$ is then computed by

\[ Q_{i, 1-\frac{\alpha }{2}}= \theta _1 \left[1 + \frac{z_{(1-\alpha /2)} \sqrt {2\theta _2h_0^2}}{\theta _1} + \frac{\theta _2 h_0 \left(h_0-1 \right)}{\theta _1^2} \right]^{\frac{1}{h_0} } \]

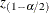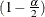where $z_{(1-\alpha /2)}$ is the $(1-\frac{\alpha }{2})$ percentile of the standard normal distribution. The lower control limit is obtained similarly by using 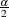$\frac{\alpha }{2}$. You can specify $\alpha $ by using the ALPHA= option in the SPECHART statement.

Multiple Observations per Time Point

When there are multiple observations at a time value in an input data set, a different approximation of the SPE distribution is used to compute control limits. The approximate distribution at time i is the scaled chi-square distribution,

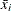\[ \frac{s_ i^2}{2 \bar{x}_ i} \, \chi _{ \frac{2 \bar{x}_ i^2}{s_ i^2} } \]

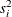where $\bar{x}_ i$ and $s_ i^2$ are the mean and variance, respectively, of the SPE statistics at time i. The upper control limit for all observations at time point i is computed as the 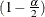$(1-\frac{\alpha }{2})$ percentile of the scaled chi-square distribution:

\[ SPE_{i, 1-\frac{\alpha }{2} } = \frac{s_ i^2}{2 \bar{x}_ i} \, \chi _{ \frac{2 \bar{x}_ i^2}{s_ i^2}, 1-\frac{\alpha }{2} } \]

Similarly the lower control limit is computed from the 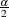$\frac{\alpha }{2}$ percentile. You can specify $\alpha $ by using the ALPHA= option in the SPECHART statement.

For more information about the distribution approximations, see Nomikos and MacGregor (1995) and Jackson and Mudholkar (1979).