XCHART Statement: CUSUM Procedure

Example 6.1 Cusum and Standard Deviation Charts

Note: See Cusum and Standard Deviation Charts in the SAS/QC Sample Library.

When you are working with subgrouped data, it can be helpful to accompany a cusum chart for means with a Shewhart s chart for monitoring the variability of the process. This example creates this combination for the variable Weight in the data set Oil (see Creating a V-Mask Cusum Chart from Raw Data).

The first step is to create a one-sided cusum chart for means that detects a shift of one standard error (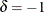$\delta =-1$) below the target mean. 

proc cusum data=Oil;
   xchart Weight*Hour /
      nochart
      mu0=8.100        /* target mean for process  */
      sigma0=0.050     /* known standard deviation */
      delta=-1         /* shift to be detected     */
      h=3              /* cusum parameter h        */
      k=0.5            /* cusum parameter k        */
      scheme=onesided
      outtable = Tabcusum
         ( drop   = _var_ _subn_ _subx_ _exlim_
           rename = ( _cusum_ = _subx_ _h_ = _uclx_ ) )
      ;
run;

The results are saved in an OUTTABLE= data set named Tabcusum. The cusum variable (_CUSUM_) and the decision interval variable (_H_) are renamed to _SUBX_ and _LCLX_ so that they can later be read by the SHEWHART procedure.

The next step is to construct a Shewhart 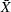$\bar{X}$ and s chart for Weight and save the results in a data set named Tabxscht. 

proc shewhart data=Oil;
   xschart Weight*Hour /
      nochart
      outtable = Tabxscht
         ( drop = _subx_  _uclx_ );
run;

Note that the variables _SUBX_ and _UCLX_ are dropped from Tabxscht.

The third step is to merge the data sets Tabcusum and Tabxscht. 

data taball;
   merge Tabxscht Tabcusum; by Hour;
   _mean_ = _uclx_ * 0.5;
   _lclx_ = 0.0;
run;

The variable _LCLX_ is assigned the role of the lower limit for the cusums, and the variable _MEAN_ is assigned a dummy value. Now, TABALL, which is listed in Output 6.1.1, has the structure required for a TABLE= data set used with the XSCHART statement in the SHEWHART procedure (see TABLE= Data Set).

Output 6.1.1: Listing of the Data Set TABALL

Obs _VAR_ Hour _SIGMAS_ _LIMITN_ _SUBN_ _LCLX_ _MEAN_ _STDDEV_ _EXLIM_ _LCLS_ _SUBS_ _S_ _UCLS_ _EXLIMS_ _subx_ _uclx_
1 Weight 1 3 4 4 0 1.5 0.05   0 0.059640 0.049943 0.11317   0.00 3
2 Weight 2 3 4 4 0 1.5 0.05   0 0.090220 0.049943 0.11317   0.00 3
3 Weight 3 3 4 4 0 1.5 0.05   0 0.076346 0.049943 0.11317   0.00 3
4 Weight 4 3 4 4 0 1.5 0.05   0 0.025552 0.049943 0.11317   0.00 3
5 Weight 5 3 4 4 0 1.5 0.05   0 0.026500 0.049943 0.11317   0.00 3
6 Weight 6 3 4 4 0 1.5 0.05   0 0.075617 0.049943 0.11317   0.30 3
7 Weight 7 3 4 4 0 1.5 0.05   0 0.037242 0.049943 0.11317   0.00 3
8 Weight 8 3 4 4 0 1.5 0.05   0 0.059290 0.049943 0.11317   0.18 3
9 Weight 9 3 4 4 0 1.5 0.05   0 0.005737 0.049943 0.11317   1.21 3
10 Weight 10 3 4 4 0 1.5 0.05   0 0.046522 0.049943 0.11317   0.62 3
11 Weight 11 3 4 4 0 1.5 0.05   0 0.040542 0.049943 0.11317   0.00 3
12 Weight 12 3 4 4 0 1.5 0.05   0 0.056103 0.049943 0.11317   0.00 3 




            

            


            
The final step is to use the SHEWHART procedure to read TABALL as a TABLE= data set and to display the cusum and s charts. 
            


ods graphics on;
title 'Cusum Chart for Mean and s chart';
proc shewhart table=taball;
   xschart Weight * Hour /
      nolimitslegend
      ucllabel = 'h=3.0'
      odstitle = title
      markers
      noctl
      split = '/'
      nolegend ;
   label _subx_ = 'Lower Cusum/Std Dev';
run;



The central line for the primary (cusum) chart is suppressed with the NOCTL option, and the default 3$\sigma $ Limits legend is suppressed with the NOLIMITLEGEND option. The charts are shown in Output 6.1.2. 
               
            

            
  

            

               
Output 6.1.2: Combined Cusum Chart and s Chart
               

               

                  
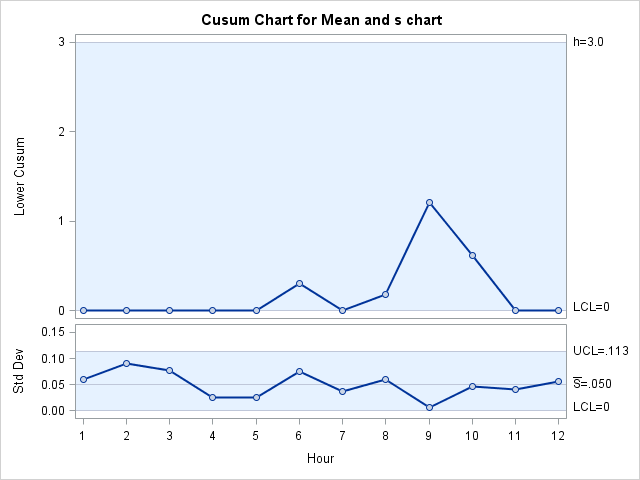
Combined Cusum Chart and  Chart

               

            

            


            
The process variability is stable, and there is no signal of a downward shift in the process mean.