SCHART Statement: SHEWHART Procedure

Creating Standard Deviation Charts from Raw Data

Note: See Standard Deviation Chart (s Chart) Example in the SAS/QC Sample Library.

A petroleum company uses a turbine to heat water into steam, which is then pumped into the ground to make oil less viscous and easier to extract. This heating process occurs 20 times daily, and the amount of power (in kilowatts) used to heat the water to the desired temperature is recorded. The following statements create a SAS data set named Turbine, which contains the power output measurements for 20 days: 

data Turbine;
   informat Day date7.;
   format Day date5.;
   input Day @;
   do i=1 to 10;
      input KWatts @;
      output;
   end;
   drop i;
   datalines;
04JUL94 3196 3507 4050 3215 3583 3617 3789 3180 3505 3454
04JUL94 3417 3199 3613 3384 3475 3316 3556 3607 3364 3721
05JUL94 3390 3562 3413 3193 3635 3179 3348 3199 3413 3562
05JUL94 3428 3320 3745 3426 3849 3256 3841 3575 3752 3347
06JUL94 3478 3465 3445 3383 3684 3304 3398 3578 3348 3369
06JUL94 3670 3614 3307 3595 3448 3304 3385 3499 3781 3711
07JUL94 3448 3045 3446 3620 3466 3533 3590 3070 3499 3457

   ... more lines ...   

23JUL94 3756 3145 3571 3331 3725 3605 3547 3421 3257 3574
;

A partial listing of Turbine is shown in Figure 17.78.

Figure 17.78: Partial Listing of the Data Set Turbine

Kilowatt Power Output Data

Obs Day KWatts
1 04JUL 3196
2 04JUL 3507
3 04JUL 4050
4 04JUL 3215
5 04JUL 3583
6 04JUL 3617
7 04JUL 3789
8 04JUL 3180
9 04JUL 3505
10 04JUL 3454
11 04JUL 3417
12 04JUL 3199
13 04JUL 3613
14 04JUL 3384
15 04JUL 3475
16 04JUL 3316
17 04JUL 3556
18 04JUL 3607
19 04JUL 3364
20 04JUL 3721
21 05JUL 3390
22 05JUL 3562
23 05JUL 3413
24 05JUL 3193
25 05JUL 3635 




            

            


            
 
            

            
The data set Turbine is said to be in "strung-out" form, since each observation contains the day and power output for a single heating. The first
               20 observations contain the power outputs for the first day, the second 20 observations contain the power outputs for the
               second day, and so on. Because the variable Day classifies the observations into rational subgroups, it is referred to as the subgroup-variable. The variable KWatts contains the power output measurements and is referred to as the process variable (or process for short). 
            

            
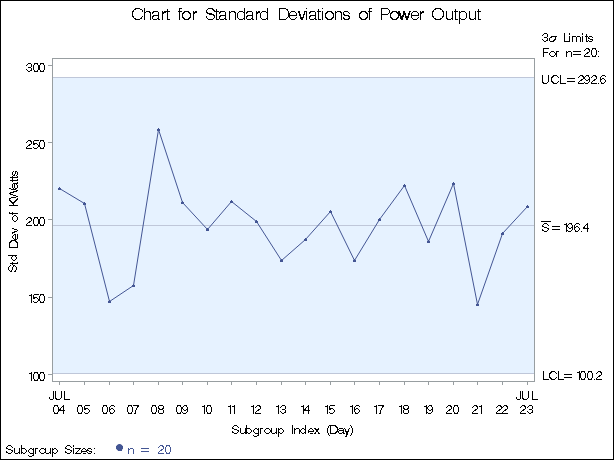
You can use an s chart to determine whether the variability in the heating process is in control. The following statements create the s chart shown in Figure 17.79: 
            


ods graphics off;
symbol v=dot h=.8;
title 'Chart for Standard Deviations of Power Output';
proc shewhart data=Turbine;
   schart KWatts*Day;
run;



This example illustrates the basic form of the SCHART statement. After the keyword SCHART, you specify the process to analyze (in this case, KWatts), followed by an asterisk and the subgroup-variable (Day). 
            

            
The input data set is specified with the DATA= option in the PROC SHEWHART statement. 

            
  

            


Figure 17.79: s Chart for Power Output Data (Traditional Graphics)
               

               

                  
Chart for Power Output Data (Traditional Graphics)

               

            

            


            
 
            

            
Each point on the chart represents the standard deviation of the measurements for a particular day. For instance, the standard
               deviation plotted for the first day is 
            

            

               
\[  \sqrt { \frac{(3196-3487.4)^{2} + (3507-3487.4)^{2} + \cdots + (3721-3487.4)^{2}}{19}} = 220.26  \]

            

            
Since all of the subgroup standard deviations lie within the control limits, you can conclude that the variability of the
               process is in statistical control. 
            

            
By default, the control limits shown are $3\sigma $ limits estimated from the data; the formulas for the limits are given in Table 17.54. You can also read control limits from an input data set; see Reading Preestablished Control Limits. 
            

            
For computational details, see Constructing Charts for Standard Deviations. For more details on reading raw data, see DATA= Data Set.