IRCHART Statement: SHEWHART Procedure

Example 17.12 Specifying Standard Values for the Process Mean and Standard Deviation

Note: See Specifying Known Values for IRCHART in the SAS/QC Sample Library.

By default, the IRCHART statement estimates the process mean ($\mu $) and standard deviation ($\sigma $) from the data, as in the previous example. However, there are applications in which known (standard) values $\mu _0$ and $\sigma _0$ are available for these parameters based on previous experience or extensive sampling.

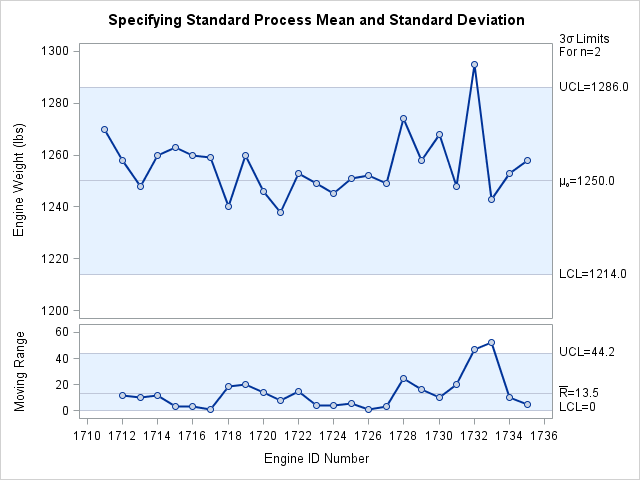
For example, suppose that the manufacturing process described in the previous example produces engines whose weights are normally distributed with a mean of 1250 and a standard deviation of 12. The following statements create individual measurements and moving range charts based on these values: 

ods graphics on;
title 'Specifying Standard Process Mean and Standard Deviation';
proc shewhart data=Engines;
   irchart Weight*ID /
      odstitle = title
      mu0      = 1250
      sigma0   = 12
      xsymbol  = mu0
      markers;
run;

The charts are shown in Output 17.12.1. The MU0= option and SIGMA0= option specify $\mu _0$ and $\sigma _0$. The XSYMBOL= option specifies the label for the central line on the individual measurements chart, and the keyword MU0 requests a label indicating that the central line is based on a standard value.

Output 17.12.1: Specifying Standard Values with MU0= and SIGMA0=

Specifying Standard Values with MU0= and SIGMA0=


You can also specify $\mu _0$ and $\sigma _0$ as the values of the variables _MEAN_ and _STDDEV_ in a LIMITS= data set. For example, the following statements create a LIMITS= data set with the standard values specified in the preceding IRCHART statement: 

data Enginelimits;
   length _var_ _subgrp_ _type_ $8;
   _var_    = 'Weight';
   _subgrp_ = 'id';
   _limitn_ = 2;
   _type_   = 'STANDARD';
   _mean_   = 1250;
   _stddev_ = 12;
run;

The variables _VAR_ and _SUBGRP_ are required, and their values must match the process and subgroup-variable, respectively, specified in the IRCHART statement. The bookkeeping variable _TYPE_ is not required, but it is recommended to indicate that the variables _MEAN_ and _STDDEV_ provide standard values rather than estimated values. See LIMITS= Data Set for details.

The following statements read Enginelimits as a LIMITS= data set: 

proc shewhart data=Engines limits=Enginelimits;
   irchart Weight*ID / xsymbol=mu0;
run;

The resulting charts (not shown here) are identical to those shown in Output 17.12.1.