The PARETO Procedure
- Overview
-
Getting Started

-
Syntax

-
Details

-
Examples
 Creating Before-and-After Pareto ChartsCreating Two-Way Comparative Pareto ChartsHighlighting the Vital FewHighlighting Combinations of CategoriesHighlighting Combinations of CellsOrdering Rows and Columns in a Comparative Pareto ChartMerging Columns in a Comparative Pareto ChartCreating Weighted Pareto ChartsCreating Alternative Pareto ChartsCustomizing Inset Labels and Formatting ValuesSpecifying Inset Headers and PositionsManaging a Large Number of Categories
Creating Before-and-After Pareto ChartsCreating Two-Way Comparative Pareto ChartsHighlighting the Vital FewHighlighting Combinations of CategoriesHighlighting Combinations of CellsOrdering Rows and Columns in a Comparative Pareto ChartMerging Columns in a Comparative Pareto ChartCreating Weighted Pareto ChartsCreating Alternative Pareto ChartsCustomizing Inset Labels and Formatting ValuesSpecifying Inset Headers and PositionsManaging a Large Number of Categories - References
Note: See Pareto Analysis Based on Cost in the SAS/QC Sample Library.
In many applications, you can quantify the priority or severity of a problem by using a measure such as the cost of repair or the loss to the customer expressed in man-hours. This example shows how to analyze such data by using a weighted Pareto chart that incorporates the cost.
Suppose that the cost associated with each of the problems in data set Failure5 (see Example 15.6) has been determined and that the costs have been converted to a relative scale. The following statements add the cost information
to the data set:
data Failure5;
length Analysis $ 16;
label Analysis = 'Basis for Analysis';
set Failure5;
Analysis = 'Cost';
if Cause = 'Contamination' then Cost = 3.0;
else if Cause = 'Metallization' then Cost = 8.5;
else if Cause = 'Oxide Defect' then Cost = 9.5;
else if Cause = 'Corrosion' then Cost = 2.5;
else if Cause = 'Doping' then Cost = 3.6;
else if Cause = 'Silicon Defect' then Cost = 3.4;
else Cost = 1.0;
output;
Analysis = 'Frequency';
Cost = 1.0;
output;
run;
The classification variable Analysis has two levels, Cost and Frequency. For Analysis=Cost, the value of Cost is the relative cost, and for Analysis=Frequency, the value of Cost is one.
The following statements use Analysis as the classification variable to create a one-way comparative Pareto chart in which the cells are weighted Pareto charts
that use Cost as the weight variable:
ods graphics off;
goptions vsize=4.25 in htext=2.8 pct htitle=3.2 pct;
title 'Pareto Analysis By Cost and Frequency';
proc pareto data=Failure5;
vbar Cause / class = ( Analysis )
freq = Counts
weight = Cost
barlabel = value
out = Summary
intertile = 1.0;
run;
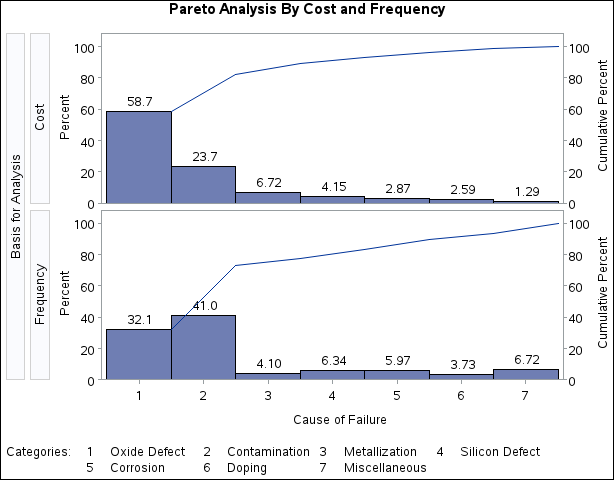
The display is shown in Output 15.8.1.
Within each cell, the height of a bar is the frequency of the category multiplied by the value of Cost, expressed as a percentage of the total across all categories. Thus, for the cell in which Analysis is equal to Frequency, the bars simply indicate the frequencies expressed in percentage units. This display shows that the most commonly occurring
problem (contamination) is not the most expensive problem (oxide defect). The output data set Summary is listed in Output 15.8.2.
Output 15.8.2: Summary Output Data Set
| Pareto Analysis By Cost and Frequency |
| Obs | Analysis | Cause | Cost | _COUNT_ | _WCOUNT_ | _PCT_ | _CMPCT_ |
|---|---|---|---|---|---|---|---|
| 1 | Cost | Oxide Defect | 9.5 | 86 | 817.0 | 58.6799 | 58.680 |
| 2 | Cost | Contamination | 3.0 | 110 | 330.0 | 23.7018 | 82.382 |
| 3 | Cost | Metallization | 8.5 | 11 | 93.5 | 6.7155 | 89.097 |
| 4 | Cost | Silicon Defect | 3.4 | 17 | 57.8 | 4.1514 | 93.249 |
| 5 | Cost | Corrosion | 2.5 | 16 | 40.0 | 2.8729 | 96.122 |
| 6 | Cost | Doping | 3.6 | 10 | 36.0 | 2.5856 | 98.707 |
| 7 | Cost | Miscellaneous | 1.0 | 18 | 18.0 | 1.2928 | 100.000 |
| 8 | Frequency | Oxide Defect | 1.0 | 86 | 86.0 | 32.0896 | 32.090 |
| 9 | Frequency | Contamination | 1.0 | 110 | 110.0 | 41.0448 | 73.134 |
| 10 | Frequency | Metallization | 1.0 | 11 | 11.0 | 4.1045 | 77.239 |
| 11 | Frequency | Silicon Defect | 1.0 | 17 | 17.0 | 6.3433 | 83.582 |
| 12 | Frequency | Corrosion | 1.0 | 16 | 16.0 | 5.9701 | 89.552 |
| 13 | Frequency | Doping | 1.0 | 10 | 10.0 | 3.7313 | 93.284 |
| 14 | Frequency | Miscellaneous | 1.0 | 18 | 18.0 | 6.7164 | 100.000 |