XSCHART Statement: SHEWHART Procedure
Example 17.43 Analyzing Nonnormal Process Data
See SHWXS4 in the SAS/QC Sample LibraryThe standard control limits for s charts (see Table 17.78) are calculated under the assumption that the data are normally distributed. This example illustrates how a transformation
to normality can be used in conjunction with ![]() and s charts.
and s charts.
The length of a metal brace is measured in centimeters for each of 20 braces sampled daily. Subgroup samples are collected for nineteen days, and the data are analyzed to determine if the manufacturing process is in statistical control.
data Lengthdata;
informat Day date7.;
format Day date5.;
label Length='Brace Length in cm';
input Day @;
do i=1 to 5;
input Length @;
output;
end;
drop i;
datalines;
02JAN86 113.64 119.60 111.66 111.88 125.29
02JAN86 114.08 115.28 127.84 109.97 109.34
02JAN86 109.65 121.76 112.17 116.01 111.64
02JAN86 112.70 114.43 110.27 114.76 125.89
03JAN86 115.92 113.62 117.52 114.44 118.08
03JAN86 111.13 118.42 112.16 112.25 107.71
03JAN86 110.46 113.78 109.89 114.59 116.98
... more lines ...
19JAN86 111.90 111.30 112.34 114.20 112.66
20JAN86 112.84 109.01 110.03 114.44 115.21
20JAN86 115.15 112.34 114.99 109.70 111.20
20JAN86 117.81 119.51 109.03 111.61 118.01
20JAN86 113.55 114.78 112.91 111.87 118.54
;
The following statements create preliminary ![]() and s charts for the lengths:
and s charts for the lengths:
ods graphics on; title 'Mean and Standard Deviation Charts for Brace Length'; proc shewhart data=Lengthdata; xschart Length*Day / odstitle = title; run;
The charts are shown in Output 17.43.1.
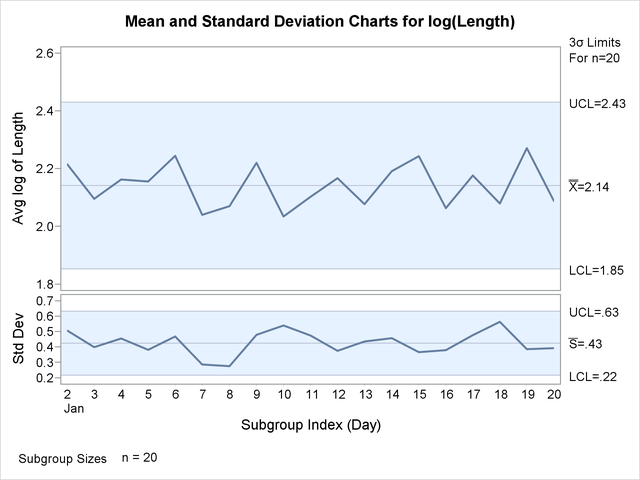
Output 17.43.1: ![]() and s Charts
and s Charts
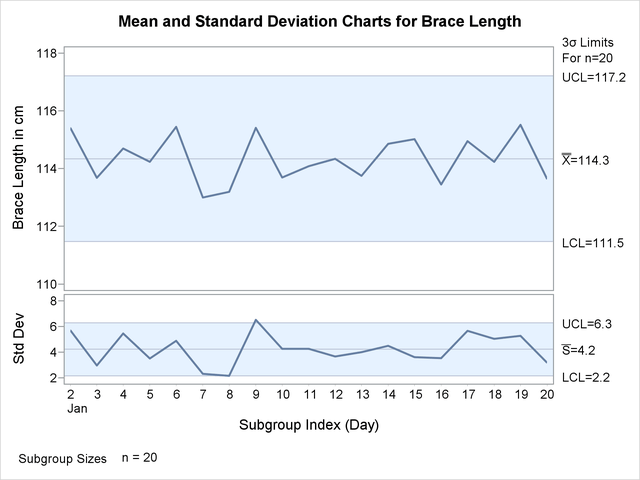
The s chart suggests that the process is not in control, since the standard deviation of the measurements recorded on January 9 exceeds its upper control limit. In addition, a number of other points on the s chart are close to the control limits.
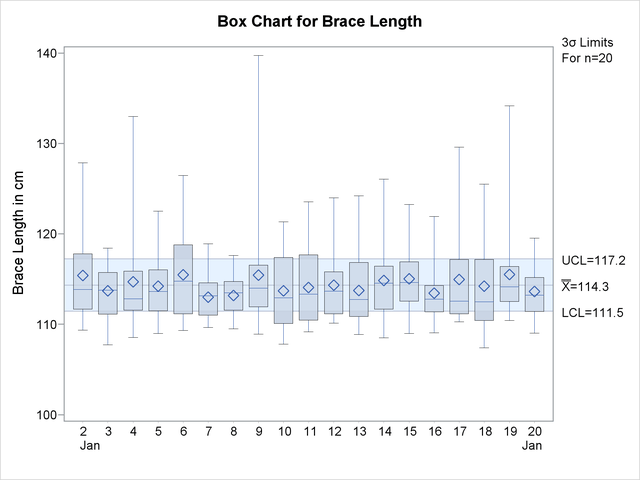
The following statements create a box chart for the lengths (for more information about box charts, see BOXCHART Statement: SHEWHART Procedure).
title 'Box Chart for Brace Length';
proc shewhart data=Lengthdata;
boxchart Length*Day / serifs
ranges
nohlabel
nolegend
odstitle = title;
run;
The chart, shown in Output 17.43.2, reveals that most of the subgroup distributions are skewed to the right. Consequently, the s chart shown in Output 17.43.1 should be interpreted with caution, since control limits for s charts are based on the assumption that the data are normally distributed.
No special cause for the skewness of the subgroup distributions is discovered. This indicates that the process is in statistical control and that the length distribution is naturally skewed.
Output 17.43.2: Box Chart
The following statements apply a lognormal transformation to the length measurements and display a box chart for the transformed data:
data Lengthdata; set Lengthdata; LogLength=log(Length-105); label LogLength='log of Length minus 105'; run;
title 'Box Chart for log(Length-105)';
proc shewhart data=Lengthdata;
boxchart LogLength*Day / serifs
ranges
nohlabel
nolegend;
run;
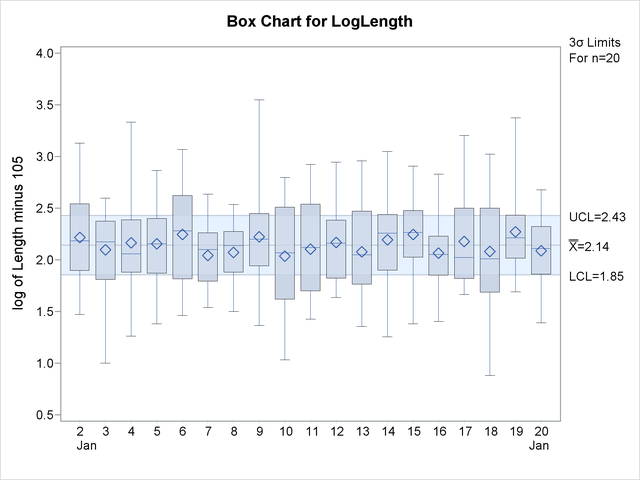
The chart, shown in Output 17.43.3, indicates that the subgroup distributions of LogLength are approximately normal (this can be verified with goodness-of-fit tests by using the CAPABILITY procedure).
Output 17.43.3: Box Chart for Transformed Data
Finally, ![]() and s charts, shown in Output 17.43.4, are created for
and s charts, shown in Output 17.43.4, are created for LogLength. They indicate that the variability and mean level of the transformed lengths are in control.
title 'Mean and Standard Deviation Charts for log(Length)';
proc shewhart data=Lengthdata;
xschart LogLength*Day / split = '/'
odstitle = title;
label LogLength='Avg log of Length/Std Dev';
run;
Output 17.43.4: ![]() and s Charts for Transformed Length
and s Charts for Transformed Length