Constructing Range Charts :: SAS/QC(R) 12.1 User's Guide

Constructing Range Charts

The following notation is used in this section:

$\sigma$	process standard deviation (standard deviation of the population of measurements)
$R_{i}$	range of measurements in ith subgroup
$n_{i}$	sample size of ith subgroup
$d_{2}(n)$	expected value of the range of n independent normally distributed variables with unit standard deviation
$d_{3}(n)$	standard error of the range of n independent observations from a normal population with unit standard deviation
$D_{p}(n)$	100pth percentile of the distribution of the range of n independent observations from a normal population with unit standard deviation

Plotted Points

Each point on an R chart indicates the value of a subgroup range ( $R_{i}$ ). For example, if the tenth subgroup contains the values 12, 15, 19, 16, and 14, the value plotted for this subgroup is $R_{10}=19-12=7$ .

Central Line

By default, the central line for the ith subgroup indicates an estimate of the expected value of $R_{i}$ , which is computed as $d_{2}(n_{i})\hat{\sigma }$ , where $\hat{\sigma }$ is an estimate of $\sigma$ . If you specify a known value ( $\sigma _{0}$ ) for $\sigma$ , the central line indicates the value of $d_{2}(n_{i})\sigma _{0}$ . Note that the central line varies with $n_{i}$ .

Control Limits

You can compute the limits in the following ways:

as a specified multiple (k) of the standard error of 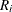$R_{i}$ above and below the central line. The default limits are computed with k = 3 (these are referred to as 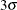$3\sigma$ limits).
as probability limits defined in terms of $\alpha$ , a specified probability that 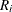$R_{i}$ exceeds the limits

The following table provides the formulas for the limits:

Table 17.48: Limits for R Charts

Control Limits
LCL = lower limit = $\mbox{max}(d_{2}(n_{i})\hat{\sigma } - kd_{3}(n_{i})\hat{\sigma },0)$
UCL = upper limit = $d_{2}(n_{i})\hat{\sigma } + kd_{3}(n_{i})\hat{\sigma }$

Probability Limits
LCL = lower limit = $D_{\alpha /2}\hat{\sigma }$
UCL = upper limit = $D_{1-\alpha /2}\hat{\sigma }$

The formulas assume that the data are normally distributed. Note that the control limits vary with $n_{i}$ and that the probability limits for $R_{i}$ are asymmetric around the central line. If a standard value $\sigma _{0}$ is available for $\sigma$ , replace $\hat{\sigma }$ with $\sigma _{0}$ in Table 17.48.

You can specify parameters for the limits as follows:

Specify k with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set.
Specify $\alpha$ with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set.
Specify a constant nominal sample size 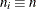$n_{i} \equiv n$ for the control limits with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.
Specify 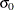$\sigma _{0}$ with the SIGMA0= option or with the variable _STDDEV_ in a LIMITS= data set.

RCHART Statement: SHEWHART Procedure

Constructing Range Charts

Plotted Points

Central Line

Control Limits