MRCHART Statement: SHEWHART Procedure
Methods for Estimating the Standard Deviation
When control limits are determined from the input data, two methods are available for estimating the process standard deviation 
.
Default Method
The default estimate for is
 |
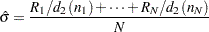where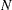 
is the number of subgroups for which 
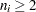, and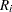 
is the sample range of the observations 
, . . . ,
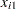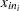in the 
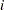th subgroup.
A subgroup range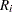 
is included in the calculation only if 
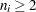. The unbiasing factor 
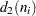is defined so that, if the observations are normally distributed, the expected value of 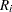is equal to 
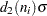. Thus, 
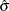is the unweighted average of 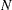unbiased estimates of . This method is described in the American Society for Testing and Materials (1976).
MVLUE Method
If you specify SMETHOD=MVLUE, a minimum variance linear unbiased estimate (MVLUE) is computed for . Refer to Burr (1969, 1976) and Nelson (1989, 1994). The MVLUE is a weighted average of 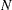unbiased estimates of of the form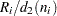 
, and it is computed as
 |
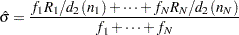where
 |
A subgroup range 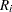is included in the calculation only if 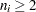, and 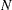is the number of subgroups for which 
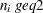. The MVLUE assigns greater weight to estimates of from subgroups with larger sample sizes, and it is intended for situations where the subgroup sample sizes vary. If the subgroup sample sizes are constant, the MVLUE reduces to the default estimate.
See Example 15.16 for illustrations of the default and MVLUE methods.