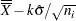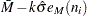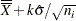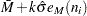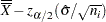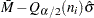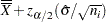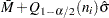BOXCHART Statement: SHEWHART Procedure
- Overview
-
Getting Started

-
Syntax

-
Details

-
Examples
 Using Box Charts to Compare Subgroups Creating Various Styles of Box-and-Whisker Plots Creating Notched Box-and-Whisker Plots Creating Box-and-Whisker Plots with Varying Widths Creating Box-and-Whisker Plots with Different Line Styles and Colors Computing the Control Limits for Subgroup Maximums Constructing Multi-Vari Charts
Using Box Charts to Compare Subgroups Creating Various Styles of Box-and-Whisker Plots Creating Notched Box-and-Whisker Plots Creating Box-and-Whisker Plots with Varying Widths Creating Box-and-Whisker Plots with Different Line Styles and Colors Computing the Control Limits for Subgroup Maximums Constructing Multi-Vari Charts
Constructing Box Charts
The following notation is used in this section:
|
process mean (expected value of the population of measurements) |
||||
|
process standard deviation (standard deviation of the population of measurements) |
||||
|
mean of measurements in |
||||
|
sample size of |
||||
|
the number of subgroups |
||||
|
|
||||
|
|
||||
|
weighted average of subgroup means |
||||
|
median of the measurements in the
|
||||
|
average of the subgroup medians:
|
||||
|
median of the subgroup medians. Denote the
|
||||
|
standard error of the median of |
||||
|
|
||||
|
|
||||
|
|
Elements of Box-and-Whisker Plots
A box-and-whisker plot is displayed for the measurements in each subgroup on the box chart. Figure 15.14 illustrates the elements of each plot.
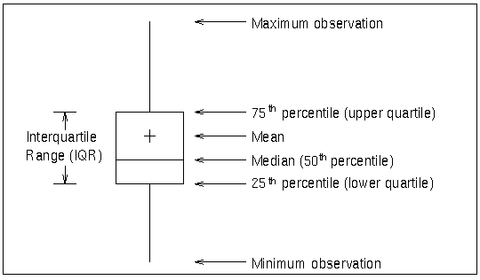
The skeletal style of the box-and-whisker plot shown in Figure 15.14 is the default. You can specify alternative styles with the BOXSTYLE= option; see Example 15.2 or the entry for BOXSTYLE= in Dictionary of Options: SHEWHART Procedure.
Control Limits and Central Line
You can compute the limits in the following ways:
as a specified multiple (
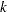 ) of the standard error of
) of the standard error of 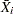 (or
(or 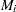 ) above and below the central line. The default limits are computed with
) above and below the central line. The default limits are computed with 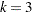 (these are referred to as
(these are referred to as 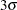 limits).
limits). as probability limits defined in terms of
 , a specified probability that
, a specified probability that 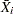 (or
(or 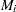 ) exceeds the limits
) exceeds the limits
The CONTROLSTAT= option specifies whether control limits are computed for subgroup means (the default) or subgroup medians. The following tables provide the formulas for the limits:
CONTROLSTAT=MEAN |
CONTROLSTAT=MEDIAN |
|---|---|
LCLX |
LCLM |
Central Line = |
Central Line = |
UCLX |
UCLM |
CONTROLSTAT=MEAN |
CONTROLSTAT=MEDIAN |
|---|---|
LCLX |
LCLM |
Central Line = |
Central Line = |
UCLX |
UCLM |
In the preceding tables, replace 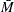 with
with 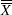 if you specify MEDCENTRAL=AVGMEAN in addition to CONTROLSTAT=MEDIAN. Likewise, replace
if you specify MEDCENTRAL=AVGMEAN in addition to CONTROLSTAT=MEDIAN. Likewise, replace 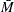 with
with 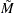 if you specify MEDCENTRAL=MEDMED in addition to CONTROLSTAT=MEDIAN. If standard values
if you specify MEDCENTRAL=MEDMED in addition to CONTROLSTAT=MEDIAN. If standard values 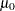 and
and 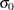 are available for
are available for 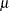 and
and  , replace
, replace 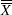 with
with 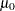 and
and 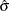 with
with 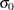 in Table 15.5 and Table 15.6.
in Table 15.5 and Table 15.6.
Note that the limits vary with 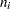 . The formulas for median limits assume that the data are normally distributed.
. The formulas for median limits assume that the data are normally distributed.
You can specify parameters for the limits as follows:
Specify
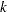 with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set.
with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set. Specify
 with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set.
with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set. Specify a constant nominal sample size
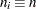 for the control limits with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.
for the control limits with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set. Specify
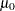 with the MU0= option or with the variable _MEAN_ in a LIMITS= data set.
with the MU0= option or with the variable _MEAN_ in a LIMITS= data set. Specify
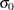 with the SIGMA0= option or with the variable _STDDEV_ in a LIMITS= data set.
with the SIGMA0= option or with the variable _STDDEV_ in a LIMITS= data set.
Note: You can suppress the display of the control limits with the NOLIMITS option. This is useful for creating standard side-by-side box-and-whisker plots.
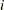 th subgroup
th subgroup 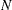
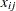
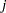 th measurement in the
th measurement in the 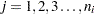
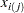
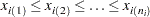
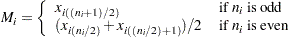
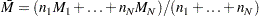
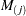 so that
so that 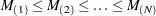 .
. 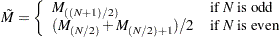
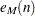
 independent, normally distributed variables with unit standard deviation (the value of
independent, normally distributed variables with unit standard deviation (the value of 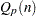
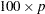 th percentile
th percentile 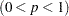 of the distribution of the median of
of the distribution of the median of 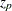
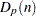
 lower limit =
lower limit =