Example 10.3 Comparison of Univariate and Multivariate Control Charts for Correlated Data
This example shows how a multivariate control chart captures changes in the correlation between a process measurement variable while univariate control charts do not. The following statements draw 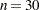 observations from the multivariate normal distribution with specified mean
observations from the multivariate normal distribution with specified mean 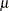 and covariance
and covariance 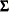 . The observations are savide in a data set named mvpStable.
. The observations are savide in a data set named mvpStable.
proc iml;
Mean = {0,0};
Cor = {1.00 0.75,
0.75 1.00};
StdDevs = {2 2};
D = diag(StdDevs);
Cov = D*Cor*D; /* covariance matrix */
NumSamples = 30;
call randseed(123321); /* set seed for the RandNormal module */
X = RandNormal(NumSamples, Mean, Cov);
varnames = { x1 x2 };
create mvpStable from X [colname = varnames];
append from X;
quit;
run;
data mvpStable;
set mvpStable;
hour=_n_;
run;
To demonstrate the effect of a change in correlation on univariate and multivariate control charts, five new observations are generated. The following statements generate data from a bivariate normal distribution with a correlation coefficient of 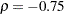 , which has the same mean and marginal variances as before.
, which has the same mean and marginal variances as before.
proc iml;
Mean = {0,0};
Cor = {1.00 -0.75,
-0.75 1.00};
StdDevs = {2 2};
D = diag(StdDevs);
Cov = D*Cor*D; /* covariance matrix */
NumSamples = 5;
call randseed(123321); /* set seed for the RandNormal module */
X = RandNormal(NumSamples, Mean, Cov);
varnames = { x1 x2 };
create mvpOOC from X [colname = varnames];
append from X;
quit;
run;
The following statements produce a data set named mvpOOC, which contains the 30 observations from the distribution with 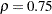 , and the five observations from the distribution with
, and the five observations from the distribution with 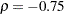 .
.
data mvpOOC; set mvpStable mvpOOC; hour=_n_; run;
The following statements build a two-component model with the MVPMODEL procedure using the mvpStable data set:
proc mvpmodel data=mvpStable ncomp=2 plots=none outloadings=loadings timegroup= hour; var x1 x2; run;
The  chart is produced by the MVPMONITOR procedure using the mvpOOC data set:
chart is produced by the MVPMONITOR procedure using the mvpOOC data set:
proc mvpmonitor data=mvpOOC loadings=loadings; time hour; tsquarechart; run;
These statements produce a  chart, shown in Output 10.3.1.
chart, shown in Output 10.3.1.
 Chart
Chart
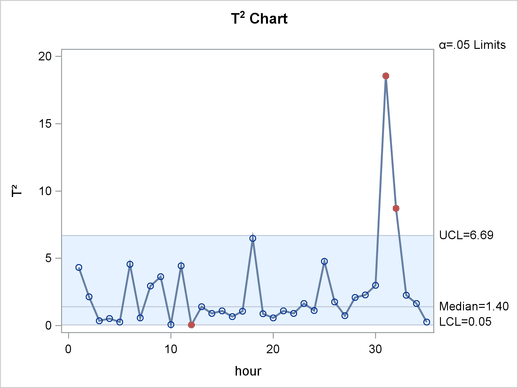
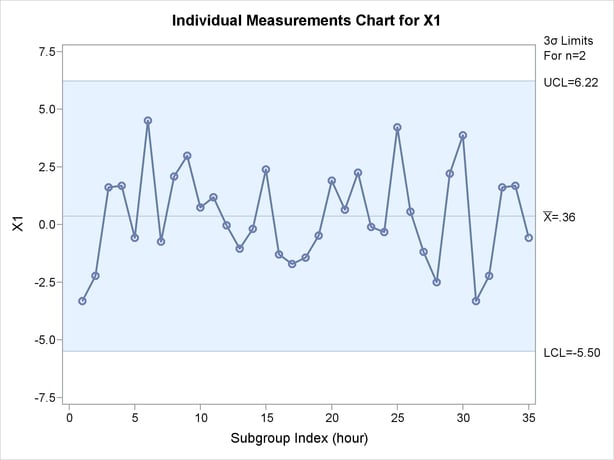
The last five points are from an out-of-control distribution resulting in some out-of-control points in the
 chart, while there are no out-of-control points in the univariate control charts shown in Output 10.3.2 and Output 10.3.3. These charts are produced with the following statements.
chart, while there are no out-of-control points in the univariate control charts shown in Output 10.3.2 and Output 10.3.3. These charts are produced with the following statements. proc shewhart data=mvpOOC; irchart (x1 x2) * hour / nochart2 markers; run;
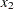
Note: This procedure is experimental.