PROC CAPABILITY and General Statements
Signed Rank Statistic
The signed rank statistic 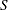 is computed as
is computed as
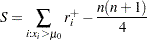 |
where 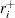 is the rank of
is the rank of 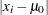 after discarding values of
after discarding values of 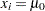 , and
, and  is the number of
is the number of 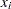 values not equal to
values not equal to 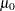 . Average ranks are used for tied values.
. Average ranks are used for tied values.
If 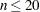 , the significance of
, the significance of 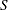 is computed from the exact distribution of
is computed from the exact distribution of 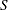 , where the distribution is a convolution of scaled binomial distributions. When
, where the distribution is a convolution of scaled binomial distributions. When 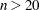 , the significance of
, the significance of 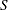 is computed by treating
is computed by treating
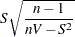 |
as a Student  variate with
variate with 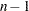 degrees of freedom. V is computed as
degrees of freedom. V is computed as
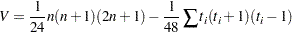 |
where the sum is over groups tied in absolute value and where 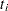 is the number of values in the
is the number of values in the 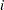 th group (Iman 1974, Conover 1980). The null hypothesis tested is that the mean (or median) is
th group (Iman 1974, Conover 1980). The null hypothesis tested is that the mean (or median) is 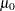 , assuming that the distribution is symmetric. Refer to Lehmann (1998).
, assuming that the distribution is symmetric. Refer to Lehmann (1998).
